Finding the unitary matrix for a beam splitter

[phb1762]

Homework Statement

(a) Construct the matrix for a beam splitter with a 70% reflectivity.
(b) By applying this operation twice, calculate the output state of a single photon in the input. Hint: the second beam splitter can be oriented in two different ways.

Relevant Equations

1) Born rule for bipartite states ( as there are 2 possibilities for input and two probabilities due to the 70:30 beam splitter)
2) ket space equations

Hello,
I have some trouble understanding how to construct the matrix for the beam splitter (in a Mach-Zehnder interferometer).

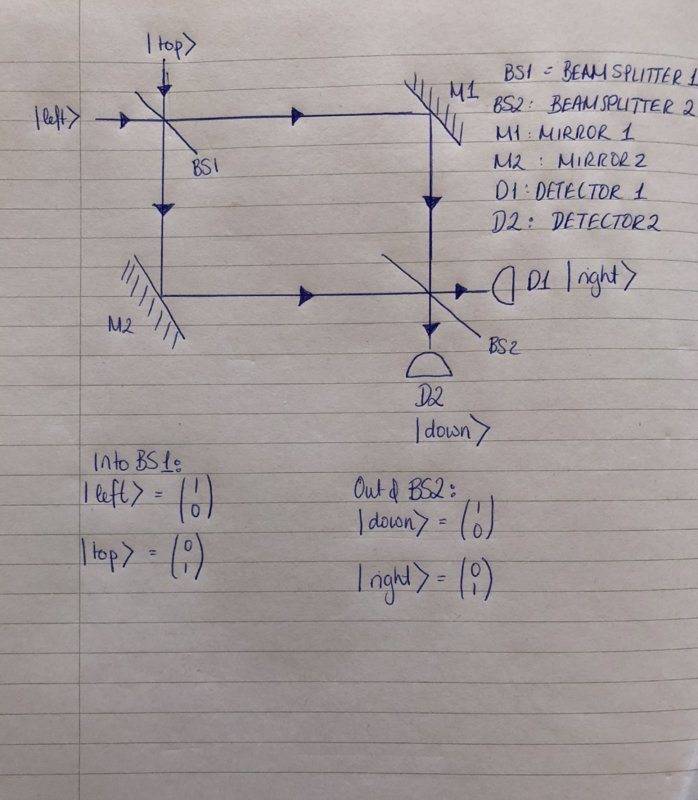
I started with deciding my input and output states for the photon.

I then use Borns rule, which I have attached below:

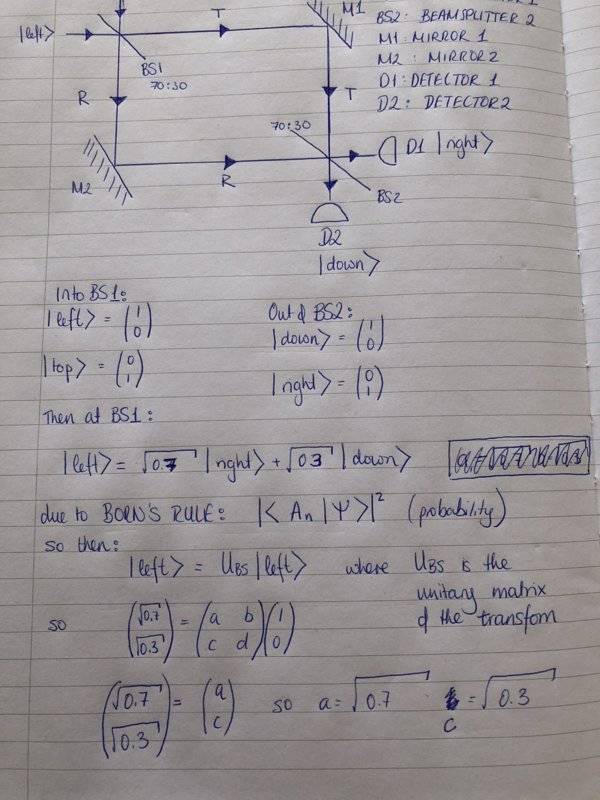
To get the following for the state space of the photon going in:

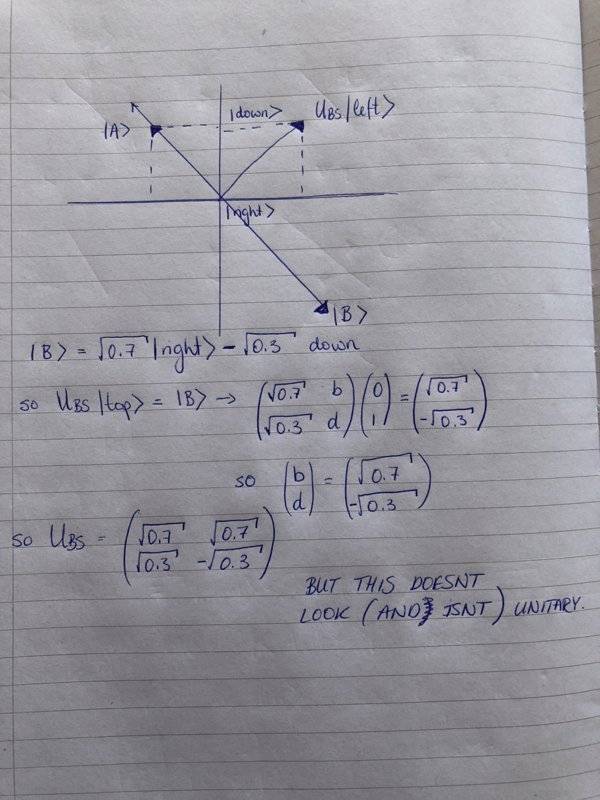
But in the end, I end up with a matrix that doesn't appear unitary:

I don’t know where I’m going wrong. We’ve only just started doing Quantum and the lectures are quite difficult for me to understand. I would appreciate any help and advice as I really would like to be able to do these types of questions as I suspect they will be in my exam!

Thanks everyone in advance and sorry for the many photos!

 

[DrClaude]

Think again about what happens at BS1 when coming in from the top.

 

[phb1762]

I really don’t understand where I’m going wrong, I thought that going in from the top should be inverse of the going in from the left?

 

[DrClaude]

If only BS1 is present, coming in from the top, was is the probability that the outcome is right?

 

[phb1762]

Ah, so something like this:

 

[DrClaude]

Ah, so something like this:

Yes. You can check now that $U_\mathrm{BS}$ is unitary.

 

[phb1762]

Yes. You can check now that $U_\mathrm{BS}$ is unitary.

Thank you so much for your time, that was very helpful!

 

[Charles Link]

Without looking at it in detail, if it is a dielectric beamsplitter with an anti-reflection (AR) coating on one side, the Fresnel coefficients for the reflectivity will be $\rho= \pm \sqrt{.70}$ and the transmission (composite) will be $\tau=\sqrt{.30}$ for both paths. The matrix method is simply a way to express the linear transformation that occurs with the Fresnel coefficients for the electric field amplitudes of the electromagnetic wave for transmitted and reflected components.
I was unaware of the matrix method for beamsplitters (developed by Schwinger) when I wrote this Insights article: https://www.physicsforums.com/insights/fabry-perot-michelson-interferometry-fundamental-approach/
If you can follow the article, you will then understand what the matrix method does.