Finding the volume of a sphere sliced by a plane

[tasveerk]

Homework Statement

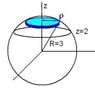
What is the volume of the region above the plane z = 2 and inside the sphere x² +y² +z² = 9.

Homework Equations

The Attempt at a Solution

I am trying to use a spherical triple integral. I am mainly having trouble finding ∅.
This is what I have been trying ∫^arccos(2/3)₀∫^2∏∫³₂ ρ²sin∅dpdθp∅
The answer is 8∏/3. I am pretty sure there are errors in my setup

 

[DryRun]

You should plot the graph to help you visualize the volume and its boundaries.
Using spherical coordinates:
\iiint {\rho}^2 \sin \phi \,.d\rho d\phi d\theta

Then describe the region (the crucial step in determining the limits):
For \phi and \theta fixed, \rho varies from \frac{2}{\cos \phi} to 3
For \theta fixed, \phi varies from 0 to \cos^{-1} \frac{2}{3}
\theta varies from 0 to 2∏

In order to get the exact answer, you need to work with the inverse angles accordingly, without using their decimal counterparts, which will obviously give you a decimal answer.

 

[tasveerk]

Would you mind explaining where you got 2/cos∅ from? Also, can you recommend a good utility to graph these functions?
Thanks!

 

[DryRun]

Would you mind explaining where you got 2/cos∅ from?
Thanks!

What is the definition of z in terms of spherical coordinates?
Example, x in terms of spherical coordinates is given by: \rho \sin \phi \cos \theta

Also, can you recommend a good utility to graph these functions?

Personally, i just draw them on paper, and i recommend you do the same, unless you're allowed to bring special graphing equipments with you in the exams.
Maybe you could try this: http://www.wolframalpha.com/
Although, i think someone else might be better able to advise you on finding the best software for graphing in 3D.

 

[ehild]

The integration would be much easier in cylindrical coordinates. The volume element can be the thin slice of thickness dz at height z with radius ρ=√(9-z²).


ehild

 

[DryRun]

Using ehild's suggestion, you would get:

\iiint rdrd\theta dz

Description of region:
For r and θ fixed, z varies from z=\sqrt{(9-r^2)} to z=3.
For θ fixed, r varies from r=0 to r=√5
θ varies from 0 to 2∏

You should get the same answer.

 

[ehild]

I meant the integral
V=\int_2^3{\int_0^{\sqrt{9-z^2}}{r \int_0^{2\pi}{d\theta}dr}dz}
which is equivalent to integrating the volume element dV=ρ²πdz with respect to z from z=2 to z=3 where ρ=√(9-z^2)

V=\pi\int_2^3{(9-z^2)dz}

ehild