Finding the Work Done in a Monatomic Ideal Gas Process

[Poulsen8r]

Homework Statement

Hi, this question is from Fundamentals of Physics 8th Edition:
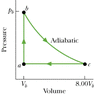
Figure 20-27 shows a reversible cycle through which 1.00 mole of a monatomic ideal gas is taken. Process bc is an adiabatic expansion, with pb = 5.20 atm and Vb = 4.80 x 10-3 m3. For the cycle, find (a) the energy added to the gas as heat, (b) the energy leaving the gas as heat, (c) the net work done by the gas, and (d) the efficiency of the cycle.

(Figure is Attached)

Homework Equations

PiVi^(Gamma)=PfVf^(Gamma)
W=P(delta)V
PV=nRT
PV^(Gamma)=nRTV^(Gamma-1)
(Delta)U=Q-W
Q=nCp(Delta)T
(Gamma)= 1.67 for monoatomic gas
Eint=(3/2)nRT

The Attempt at a Solution

This may look a little weird because of the subscript and powers but i'll give it a go:
Calculating Pressure at (a) and (c):
PiVi^(Gamma)=PfVf^(Gamma)
5.2689e5*4.8e-3=Pf*38.4e-3
Pf=1.6352e4 Pascals

Calculating Work from c to a:
W=P(delta)V
=1.6352e4*(38.4-4.8)e-3
=549.4272J

I believe this is correct...

Calculating temperature at (b) and (c):
T=(PV^(Gamma))/(nRV^(Gamma-1))

Tb=((5.2689e5)*(4.8e-3)^1.67)/(1*8.314*(4.8e-3)^(-0.67))
=304.1944K

Tc=((1.6352e4)*(38.4e-3)^1.67)/(1*8.314*(38.4e-3)^(-0.67))
=75.5233K

Calculating (Delta)Eint for process b to c:
(Delta)Eint=nRTf-nRTi
=nRTc-nRTb
=(1*8.324*75.5233)-(1*8.314*304.1944)
=-2851.757J --> I think this is where the problem lies.

Calculating work for process b to c:
(Delta)Eint=Q-W, as it is adiabatic Q=0 therefore (Delta)Eint=-W.
W=2851.757J

As there is no work for the process a to b, this means that the net work done on the system is 3401.18J... Which is incorrect... I don't know the solution but i know that that answer is wrong... I tried a few other methods than the one above but i get the same answer and i am going crazy and in circles...

 

[Andrew Mason]

Calculating Work from c to a:
W=P(delta)V
=1.6352e4*(38.4-4.8)e-3
=549.4272J

You can't do it this way. You have to integrate to find the area under the curve from c to a. It is not a rectangle.

Use:

TV^{\gamma - 1} = K to find the change in temperature from c to a. Since there is no added heat, you know that W = -\Delta U = -nCv\Delta T

AM

 

[Poulsen8r]

You can't do it this way. You have to integrate to find the area under the curve from c to a. It is not a rectangle.

Use:

TV^{\gamma - 1} = K to find the change in temperature from c to a. Since there is no added heat, you know that W = -\Delta U = -nCv\Delta T

AM

But why is the work done from c to a not a rectangle? i mean Work is the area under the graph which for the line c to a is a rectangle. And how can we apply the Constant volume formulas when its not at a constant volume? Also how do we know there's no added heat?