Finding torque/tension in pulley/block system.

[SteelDirigibl]

Homework Statement

I just had my physics final... doing this from memory, so if you think I have left something out let me know.
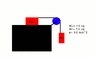
Basically we have a setup like the attached diagram. frictionless surface up top, masses of the hanging block is 5 kg, and the other block is 3 kg. acceleration of this system is 4.0 m/s²
I realize I forgot to label the tensions, but I was to find the tension of the string "above" (before) the pulley, as well as the tension of the string from which M2 is hanging. Let's call these tensions T1 and T2 respectively.

I was then to find the torque on the wheel.

The last thing I was to do is find the value for the ratio I/R² where R is the radius, and I assumed I was meant to be inertia. I assume this would give mass of the pulley?

Homework Equations

I=mR²
F=ma
\tau=I\alpha

The Attempt at a Solution

First, to find tension in T1 (the top part of string) I simply did F=ma, or 3*4=12N
For the second tension, I did F=mg-ma, or 9.8*5-4*5, 5*(9.8-4)=29N

I'm fairly sure of these parts. So for the torque on the pulley, it would just be the difference in these two tensions, 17N?

From there, we have the torque equation, and say 17N=I*4
hmm now that I wrote that down it seems wrong. And I seem to recall simply doing 17/4 and saying that was I/R, or 4.25 kg. which I feel is wrong... so... now what? if for only the sake of knowing why I was wrong...

 

[collinsmark]

I'm fairly sure of these parts. So for the torque on the pulley, it would just be the difference in these two tensions, 17N?

You need to multiply that times the radius if you are trying to convert it to a torque. The net tangential force on the pulley is 17 N, but to convert that to a torque you need to multiply it times the radius of the pulley, R.

\vec \tau = \vec R \times \vec F

Because the force is tangential already, the magnitude of the torque is simply τ = RF.

From there, we have the torque equation, and say 17N=I*4

As mentioned above, the left hand side of the equation needs to be multiplied by R.

On the right hand side of the equation, you are multiplying I by the linear acceleration. But you need to multiply it by the angular acceleration: α = a/R.

Note that the Rs do not cancel out. Instead, you get an R² in there somewhere.

hmm now that I wrote that down it seems wrong. And I seem to recall simply doing 17/4 and saying that was I/R, or 4.25 kg. which I feel is wrong... so... now what? if for only the sake of knowing why I was wrong...

The ratio of F/a = (17 [N])/(4 [m/s²]) = 4.25 [kg] is related to the mass of the wheel/pulley. But it depends on the shape/configuration of the wheel/pulley. (You haven't given us enough information on the wheel/pulley).

If your final, numerical answer specified that 4.25 [kg] was the mass of the wheel/pulley:

• If the pulley was more-or-less in the shape of a hoop, your (numerical) answer looks quite good.
• If the pulley was more-or-less in the shape of a solid disk, your (numerical) answer looks only about ½ good.

 

[SteelDirigibl]

ok so 17*R=I*4/R, right? where 4/R is the angular acceleration. Then I can divide the R over from the far side, so you have 17=I*4/R²

When you divde the four back out, you are left with 17/4=I/R²=4.25

this is the ratio it asked for in the question, and is equal to 4.25
Notice the original question did not mention mass of the pulley, that was just what I though the ratio represented, which may or may not be true.

So it looks like, my numerical answer is correct, however, it is not the mass as I thought it was?
I am still a little confused since I=mR² and with that ratio the R's DO cancel, leaving you with just m? And I am no longer sure now what is correct. Using the formulas and procedures you stated, I still found a numerical value for I/R², and I also found I/R².
I must still be missing something, because we seem to be agreeing on procedures but disagreeing somewhere else...

It may be worth noting I was also not given a radius.

 

[collinsmark]

ok so 17*R=I*4/R, right? where 4/R is the angular acceleration. Then I can divide the R over from the far side, so you have 17=I*4/R²

When you divde the four back out, you are left with 17/4=I/R²=4.25

There you go. That fixed it up.

this is the ratio it asked for in the question, and is equal to 4.25
Notice the original question did not mention mass of the pulley, that was just what I though the ratio represented, which may or may not be true.

So it looks like, my numerical answer is correct, however, it is not the mass as I thought it was?

It is if the pulley is hoop shaped. But it's not if the pulley is some other shape, such as a solid disk. You didn't give us the mass distribution of the pulley in the problem statement, so I don't know what it is. More on that below.

I am still a little confused since I=mR² and with that ratio the R's DO cancel, leaving you with just m?

It's true that I = mR² if the pulley is shaped like a hoop.

But if the pulley is shaped like solid disk, the moment of inertia is I = ½mR²

On the other hand, if the pulley is shaped like a solid sphere, the moment of inertia is I = 2mR²/5. For a hollow sphere, I = 2mR²/3.

Here is a link that gives you a list of moments of inertia of common shapes:
http://en.wikipedia.org/wiki/List_of_moments_of_inertia"

And I am no longer sure now what is correct. Using the formulas and procedures you stated, I still found a numerical value for I/R², and I also found I/R².
I must still be missing something, because we seem to be agreeing on procedures but disagreeing somewhere else...

I don't think we're really in disagreement. It's just that I can't verify whether 4.25 kg is the mass of the pulley without knowing how the pulley is shaped.

If the pulley is hoop shaped, then

4.25 kg = I/R² = mR²/R² = m.​

So in that case, yes, the mass of the pulley is 4.25 kg.

But if the pulley is shaped like a solid disk,

4.25 kg = I/R² = ½mR²/R² = ½m.​

So in that case, the mass of the pulley is 8.5 kg.

But it sounds to me as though the lab problem wasn't asking for the mass of the pulley. Rather it was just asking for I/R². And from what I can tell, you seem to have gotten that correct.

 

[SteelDirigibl]

ok this makes sense. There is no mention of the shape of the pulley, which is why it was left in the form I/R²
Had I been given more information, could have determined mass of the pulley, but without knowing for sure, I can't really say it is the mass, just the ratio I/R²

All seems clear now and it looks like I did it right, however I may lose a few points for assuming this would be the mass of the pulley.

Gosh this is a great forum it's too bad I waited for the final to join. You all will be seeing me in the Spring semester :)