Infernorage
- 24
- 0
Homework Statement
Let F=xi-yj+zk and the pyramid be as shown below. Find \iint\limits \,F\bullet dS as a surface integral over all five faces.
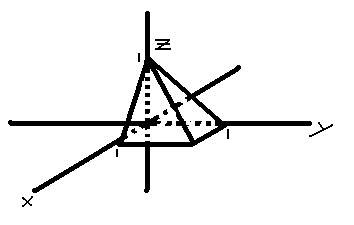
The attempt at a solution
I first solved it using the divergence theorem. The divergence was just 1, so the answer should just be the volume of the pyramid, which is 1/3, right?
I think that the normal vectors of the two angled faces are i+k and j+k, but I don't understand how to find the dS or the limits of integration since no real equation was given for the surface. Tried doing the surface integrals of the two angled faces assuming that the two angled faces were the intersection of the surfaces z=1-x and z=1-y, but my answer is not coming out to 1/3. The flux through the non-angled faces (left, back, and bottom) should just be zero, right? I don't know whether I am just not seeing it or what, but can you guys help me out? Thanks in advance.
Let F=xi-yj+zk and the pyramid be as shown below. Find \iint\limits \,F\bullet dS as a surface integral over all five faces.
The attempt at a solution
I first solved it using the divergence theorem. The divergence was just 1, so the answer should just be the volume of the pyramid, which is 1/3, right?
I think that the normal vectors of the two angled faces are i+k and j+k, but I don't understand how to find the dS or the limits of integration since no real equation was given for the surface. Tried doing the surface integrals of the two angled faces assuming that the two angled faces were the intersection of the surfaces z=1-x and z=1-y, but my answer is not coming out to 1/3. The flux through the non-angled faces (left, back, and bottom) should just be zero, right? I don't know whether I am just not seeing it or what, but can you guys help me out? Thanks in advance.