DaveC426913
Gold Member
2025 Award
- 24,218
- 8,341
Since he has a naive understanding of GR in the first place, he's not going to follow the logic of equations.
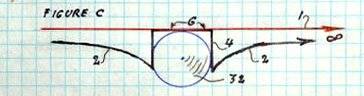
But he has produced some diagrams, at my behest. Here is one of a hollow sphere, which has some unexplainable cusps and nigh-infinite slopes:
I have started showing him the logical implications of his idea that lead to paradoxes. (Such as a watch on one wrist running at a dramatically different rate than the watch on the other wrist).
He has, predictably, begun to lose interest and wander away, mumbling about 'paradoxes' in Einsteinian models.
If anyone is interested in the dialogue, it is here:
http://www.sciforums.com/threads/where-is-most-gravity-inside-or-out.155498/page-8#post-3512088
poster's name is nebel.
But he has produced some diagrams, at my behest. Here is one of a hollow sphere, which has some unexplainable cusps and nigh-infinite slopes:
I have started showing him the logical implications of his idea that lead to paradoxes. (Such as a watch on one wrist running at a dramatically different rate than the watch on the other wrist).
He has, predictably, begun to lose interest and wander away, mumbling about 'paradoxes' in Einsteinian models.
If anyone is interested in the dialogue, it is here:
http://www.sciforums.com/threads/where-is-most-gravity-inside-or-out.155498/page-8#post-3512088
poster's name is nebel.