Flight Mechanics - Range and Payload calculations

[DanRow93]

Homework Statement

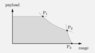
Assume that m(fuel, climb) = 1300kg is the mass of fuel required for the climb to the cruising altitude of 10,000m, independently of the take-off weight. Assume that the distance covered during the climb is always 100km. Consider the typical payload-range diagram shown and calculate the values of the payload and range at points P1, P2 and P3. Ignore the descent phases.

https://imgur.com/tgdNBUC

Some necessary variables:

TSFC = 0.63 h^(-1)

m(empty) = 8600kg

m(max take-off) = 14000kg

m(max fuel) = 5200kg

m(max payload) = 1400kg

AR = 11.02083

CD(0) = 0.016

CL(max) = 1.4

e = 0.84

S = 48 m^(2)

p (density) = 0.414 at 10,000m

g = 10 m/s^(2)

W0 = Initial weight of aeroplane (with fuel)

W1 = Final weight of aeroplane (all fuel used)

Homework Equations

R = (1/TSFC)*(√(8/(pS)))*((CL^(0.5))/CD)*(√W0 - √W1)

CL: This is where I may have made a mistake, I assumed that because the Range formula above contains "((CL^(0.5))/CD)", I should calculate CL using the bottom formula in this image: https://imgur.com/DpAFSEJ

CL = √((Pi/3)*e*AR*CD(0))

CD = CD(0) + (CL^(2))/(Pi*e*AR)

The Attempt at a Solution

Firstly, these are the places where I have possibly gone wrong:

1. Question states that m(fuel, climb) is independent of the take-off weight. Does this mean that I ignore it and don't use it at all in finding the value of W0?

2. CL in the Range formula. Possible that I just use the given value CL(max) to find the points (the points on the diagram are maximum ranges)?

3. I may have worked out W0 and W1 wrong. I believe W0 = W(max take off) - W(fuel climb), and W1 = W(empty) + W(payload).

Attempt:
P1 is the point at which range is maximum with W(max payload).

Payload = m(max payload) = 1400kg

W0 = W(max take-off) - W(fuel, climb) = (m(max take-off)*10) - (m(fuel,climb)*10)
= 140000 - 13000 = 127000N

W1 = W(empty) + W(max payload)
= (8600*10) + (1400*10) = 100000N

CL = √((Pi/3)*e*AR*CD(0))
= √((Pi/3)*0.84*11.02083*0.016) = 0.39384

CD = CD(0) + (CL^(2))/(Pi*e*AR)
= 0.016+(0.39384^(2))/(Pi*0.84*11.02083) = 0.02133

R = (1/TSFC)*(√(8/pS))*((CL^(0.5))/CD)*(√W0 - √W1)
= (1/0.63)*(√(8/(0.414*48)))*((0.39384^(0.5))/0.02133)*(√127000 - √100000)
= 1189.48966 km

+100km (distance covered during climb) = 1289.48966 km

 

[.Scott]

1. Question states that m(fuel, climb) is independent of the take-off weight. Does this mean that I ignore it and don't use it at all in finding the value of W0?

Basically, yes.
Your takeoff weight can be anything from 8600 to 14000 Kg. Since you need 1300 Kg to climb to 10Km, we only need to consider 9900 to 14000 Kg. And since we are only looking for maximum ranges, we only need to look at 13800 to 14000 Kg. In reality, the amount of fuel you would consume to climb to 10Km would be a function of how much you started with - since lifting fuel into the sky takes fuel. But they are saying that is not the case for these problems. It will be 1300 Kg in all cases. Assuming no payload (and no pilot), when you reach 10Km, your aircraft will weigh from 8600 to 12700 Kg.

2. CL in the Range formula. Possible that I just use the given value CL(max) to find the points (the points on the diagram are maximum ranges)?

CL is the lift coefficient. I get the same number as you.

3. I may have worked out W0 and W1 wrong. I believe W0 = W(max take off) - W(fuel climb), and W1 = W(empty) + W(payload).

I agree. That would be the W0 and W1 for the level segment of the flight.
I also don't see anything wrong with the rest of your calculations.

For the next two steps, set the payload to 200 Kg and 0 Kg. In both of those cases you will be using maximum fuel (5200 Kg).

 

[DanRow93]

Basically, yes.
Your takeoff weight can be anything from 8600 to 14000 Kg. Since you need 1300 Kg to climb to 10Km, we only need to consider 9900 to 14000 Kg. And since we are only looking for maximum ranges, we only need to look at 13800 to 14000 Kg. In reality, the amount of fuel you would consume to climb to 10Km would be a function of how much you started with - since lifting fuel into the sky takes fuel. But they are saying that is not the case for these problems. It will be 1300 Kg in all cases. Assuming no payload (and no pilot), when you reach 10Km, your aircraft will weigh from 8600 to 12700 Kg.

CL is the lift coefficient. I get the same number as you.
I agree. That would be the W0 and W1 for the level segment of the flight.
I also don't see anything wrong with the rest of your calculations.

For the next two steps, set the payload to 200 Kg and 0 Kg. In both of those cases you will be using maximum fuel (5200 Kg).

I have put these as my answers (online homework), and my three values for range are wrong. Values for payload (1400, 200, 0) are correct.

The only thing that I can spot that might be the reason is that we are given CL(max) in the known variables. Perhaps I am supposed to use it in the range equation instead of calculating CL? So (1.4^(0.5))/CD

Edit: That gave me a much lower number for Range. I'm out of ideas.

 

[.Scott]

The only thing that I can spot that might be the reason is that we are given CL(max) in the known variables. Perhaps I am supposed to use it in the range equation instead of calculating CL? So (1.4^(0.5))/CD

Cl(max) occurs when the angle of attack is very large - just before the plane goes into a stall. So it makes no sense to use that value. Operating the plane at Cl(max) is a good flight exercise for the pilot, but it does not provide good range - quite the opposite.

When you plugged in the value for 200, your takeoff weight was 13800 and your W0 was 12500, right?