- #1
kmot
- 7
- 1
Hi,
In a text describing solution to linearized shallow water equations, I am not able to move forward.
It's a 1 dimensional shallow water setup. There is a steady state
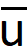(velocity) and
(height of free surface). On top of this steady state there are u' and h' as disturbances. The goal is to solve for h'(x,t)
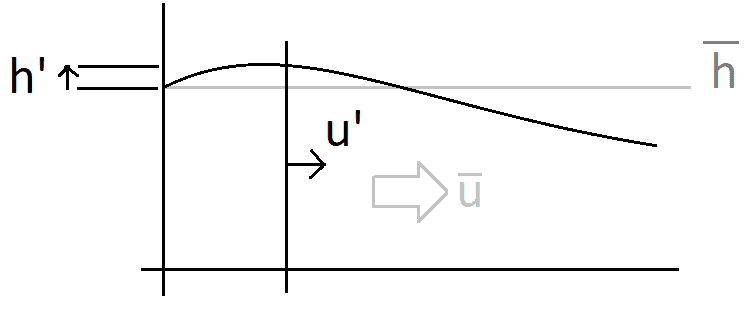
The governing equations are:
(1)
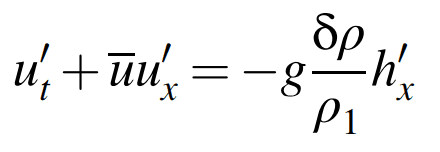(momentum)
(2)
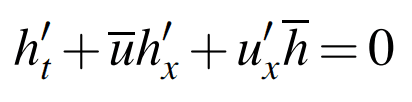(mass continuity)
Subscripts denote partial derivatives.
The text says these two can be combined to arrive at wave equation, without providing further details of how:
(3)
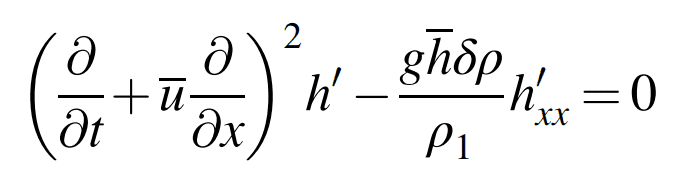
But with anything I tried I wasn't able to eliminate u' completely. I'm always left with a term including u' in (3). Perhaps the term that can't be eliminated can be neglected, but I don't see why.
Would somebody be willing to provide a step by step guide how to go from (1) & (2) to (3), including reasoning of why something can be neglected (if neglecting is needed)?
Thank you very much
In a text describing solution to linearized shallow water equations, I am not able to move forward.
It's a 1 dimensional shallow water setup. There is a steady state
The governing equations are:
(1)
(2)
Subscripts denote partial derivatives.
The text says these two can be combined to arrive at wave equation, without providing further details of how:
(3)
But with anything I tried I wasn't able to eliminate u' completely. I'm always left with a term including u' in (3). Perhaps the term that can't be eliminated can be neglected, but I don't see why.
Would somebody be willing to provide a step by step guide how to go from (1) & (2) to (3), including reasoning of why something can be neglected (if neglecting is needed)?
Thank you very much
Last edited: