Force Couple Problem (Thrust of Ship)

[Ratiocinator]

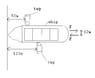
I am having difficulty in understanding the solution to the problem described below and illustrated by a rather crude Paint sketch I made:


“Each propeller of the twin-screw ship develops a full-speed thrust of 600kN. In maneuvering the ship one propeller is turning full speed ahead and the other turning full speed in reverse. What thrust P must each tug boat exert on the battleship to counteract the turning effect of the ship’s propellers?”This is the answer:P = 600 * 12 / (120 – 50) = 102.86kNSurely the distance of the tug boats from the thrusters should matter (easier to combat the turning force of the ship’s propellers the farther away the tugs are from it, so as to take advantage of leverage / mechanical advantage)? And does not the precise location of the center of thrust of the ship’s propellers matter?

I assume one tug is pushing and the other pulling.

Also, how does the answer and solution provide the amount of thrust for each tugboat and not just a figure of total force needed to counter the turning effect of the ship’s propellers?

Another point: The question and answer only seems to care about the difference that each tug has in relation to each other from a reference point, which in this case is a plane perpendicular with the bow of the ship (70m). But should the tugs be the same distance from this reference point then the moment of the ship’s propellers would be divided by zero, which of course would render zero as the final answer! Obviously, in real life, the answer would not be zero if the two tugs were the same distance from the reference point.

I am having a very hard time trying to understand this simple problem. Any explanation to help clear my brain fog would be much appreciated!

Edit: Direct link to diagram, as attachment is pending approval:

http://img440.imageshack.us/img440/3025/staticsshiplq6.gif

 

[Kenny Lee]

Hi Ratio,

I'm having trouble understanding some of your questions, but when dealing with statics problems, I usually just do the following: set force and moment equilibrium equations and solve.

Force equilibrium in X gives n'o meaningful results so we skip

FOrce equlibrium in Y tells us that the forces at the bottom and top tug boats are equal and opposite

This is probably the most important: we note that the twin thrusters produce a clockwise moment couple of 600 kN X 12 m. Maybe you know this, but just in case, a moment couple occurs when there are two opposite but equal parallel forces that are not collinear; the size of the moment is thus given by the product of the force and distance between. (that make sense? =) )

So setting moment equilibrium about any point on the left vertical, we get: 600 X 12 + 50P - 120P = 0

REarranging for P gives the answer.

Did that help?
.....
Kenny

 

[Ratiocinator]

Thank you for your reply. What you posted is helpful, but unfortunately there are still things about this problem (and the like) that I fail to understand.

I still do not know why just the difference in distance between the two tugs from a reference point (a reference point that could be anywhere at all, even three miles away!) is the only crucial part of the calculation (the calculation to counter the twin-propeller thrust)? And I still do not understand how the solution renders a force figure for each tug and not just a total figure?

I would have thought that the force of the turning ship would differ along its length. So I would have thought the distance of the tugs from the ship’s propellers to be vital to the calculation, but they are totally ignored!

 

[Kenny Lee]

Hi,

You're prolly thinking in terms of 'what force P is required to counteract the moment couple at the end of the boat'. This is right, but I find the most systematical way to think of this is that every force contributes a moment, and the sum of all these moments about some reference point (it doesn't matter where, as long as we pick one and stick with it), must equal to zero for static equilibrium (no acceleration). So what we have is this:

50 T - 120 T + 6F + 6F = 0

Where T is the force on the tugs, and F is the force from the propellers; and
I have taken the reference point to be at the bow of the boat, so that the perpendicular distance from the point of thrust to the reference is 6, and 50 and 120 for the top and bottom tugs respectively.
Notice that I have skipped using the moment couple shortcut - hopefully this will make it clearer. So now what you got to do is substitute F and solve for T.

You see what I'm getting at? the reference point can be anywhere as long as its consistent throughout the calculation, because it wouldn't make a difference mathematically.

I'm not sure what you mean exactly by having a total figure for force. Each tug is going to exert a force of its own, so its natural for there to be separate forces.

As for forces differing along the length... you are right, but these are internal forces i.e. the forces within the rigid body in question: the boat; and Newton's laws apply to external forces like the thrust and tugs. There are no external forces along the boat.

Does that help?
Hopefully i didn't repeat anythign from my earlier post.

Kenny

 

[Ratiocinator]

Thanks again, but I still do not feel that I have grasped this problem, even though I could just parrot this technique to provide answers to similar questions.

I do not understand the internal and external forces differences here. All I see is a turning force created by the two propellers, and I feel that the force required to combat that turning force, the aim of the question, would be different depending upon how far this counter force is applied from the propellers.

If there was only a single tug how could I calculate the force it would need to exert upon the side of the ship in order to counter the turning force of the ship’s propellers? Would the distance that tug be from the propellers not be fundamental to finding the answer?

I am still confused as to why only the difference in distance between the two tugs from the reference point matters, and not the difference the tug(s) are from the ship’s propellers?

I think maybe a more simplified explanation could be the key to my understanding this!

 

[Kenny Lee]

"All I see is a turning force created by the two propellers, and I feel that the force required to combat that turning force... would be different depending upon how far this counter force is applied from the propellers"

*Actually, no, the moment couple caused by the propellers can be anywhere on the boat and you'd still get the same answer. That's because the moment couple produces the same turning force about any point (thats what's unique about it). If say the turning moment at the propellers were not caused by a moment couple, but a vertical force, then certainly, the value of P would depend on the distance between (like a balance beam).

*You can't have a single tug, cause then you can't satisfy force equilibrium in y.

Hopefully that clears things up.

 

[Ratiocinator]

If only a single tug were involved, then I guess the ship would just pivot around it? Is that right?

If there was a fixed pivot between (in the middle of) the two propellers then one tug could be used to counter the turning effect of the ship, and in such a situation the distance of the tug(s) from the ship’s propellers would be crucial? Is that correct?

I am still having difficulty comprehending this unique feature of force couples. I find it odd that the magnitude of the turning force is the same throughout the entire length of the ship. So, should the ship be 100-miles long, then the tugs would need to exert the same amount of force, and use the same amount of energy, to counter the force of the ship’s propellers and stop the ship from turning 100-miles from the propellers as they would if they were just 2 meters from the propellers?

Thanks.

 

[Kenny Lee]

Maybe this will help?

http://imgcash2.imageshack.us/img234/59/momentcoupleva5.jpg

You can take moment about any point, and you'd still get FD.

I just suck at explaining

K then, good luck