Force exerted on counter-rotating wheels by a tennis ball

[ballboy]

Homework Statement

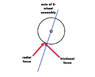
I am trying to figure out what torque is applied to 2 wheels counter-rotating at 4,000 rpm when a tennis ball is squeezed between them and then propelled forward (because the wheels are counter-rotating).This is how a tennis ball machine propels a ball forward. I know the distance between the edge of the counter-rotating wheels and I know how much force it takes to compress the tennis ball so it fits between the wheels, ie about 60 lbs, so I guess that's 30 lbs on each wheel. The traditional formula of Torque = Distance * Force * sin(theta) does not work because the force is being applied in line with the radius against the edge of each wheel towards the axle. Sin (0 deg) or sin (180 deg) in that equation are 0 so the equation yields 0 torque but that cannot be the case. It's kind of like applying breaks to the wheels of a car but not stopping. Radius of the wheel is 3".

Does anyone know? Maybe there is a way to translate perpendicular force against the wheel edge into tangential force when the wheel is rotating at a certain rpm?

Homework Equations

Torque = Distance (ie radius) * Force * sin(angle)

The Attempt at a Solution

Torque = 3 in * 30 lbs * sin(180) = 90 * 0 = 0

But it can't be zero and also doesn't the rpm figure in somehow?[/B]

 

[scottdave]

So if it is 6 pounds force to compress it (likw you'd push against a surface) then the surface is also pushing back with 60 lbf. So it is not 30 pounds per wheel, it would be 60 each.

 

[ballboy]

Ok I guess each side of the ball then is exerting 60 lbs of force on each wheel, but even using 60 the answer using my equation is still 0.

 

[haruspex]

Ok I guess each side of the ball then is exerting 60 lbs of force on each wheel, but even using 60 the answer using my equation is still 0.

Interesting problem.
Consider some stage during compression. Draw a diagram. You have the centres of the wheels, A and B, the centre of the ball C, and (the centres of) the points of contact between the ball and the wheels, D and E.
At the contacts there is a normal force and a frictional force.
There is a relationship between the angle ABE and the distance DE. The hard part is figuring out the relationship between that distance and the normal forces on the ball. You will need to assume some model for how the ball deforms.

 

[ballboy]

I did that. Let's just consider the worst case scenario where the greatest force is being applied to the wheels at that would be at the point at which the origin (center point) of the tennis ball is on the same line as one drawn between the origin of both wheels as shown in the diagram I drew below. 60 lbs force is being exerted on each wheel at this point as that's what it takes to compress the ball until it fits between the wheel before it shoots out the other side. The deformation of the tennis ball is equal on both sides. That is the torque applied to each wheel by the resisting forces of 60 lbs on each side of the ball?

ABE is not an angle, but a straight line. The force is perpendicular to each wheel surface.

This seems like a simple problem that arises all the time. There must be a simple formula for it.

 

[haruspex]

did that. Let's just consider the worst case scenario

No, that's not the diagram I indicated. I said "at some point". As you already found, what you have drawn does not involve any torque, so it is certainly not the worst case. Draw a diagram for an arbitrary earlier point, where the force is still increasing.

 

[ballboy]

OK, I am not understanding something. Would not the force on the wheels be the greatest when the ball is compressed the most, ie as in the diagram? As the ball just enters between the wheels and starts touching them the wheels won't be compressing the ball hardly at all so wouldn't there be very little torque exerted on the wheels? Also, it's harder to slow down a wheel that is moving faster than one that is moving slower so does not the rpm of the wheels also come into play?

Where does the ball have to be for the torque exerted on the wheels to be the greatest then?

 

[haruspex]

Would not the force on the wheels be the greatest when they have to be compressed the most?

Yes, but that force is radial to wheels, so exerts no torque.

Where does the ball have to be for the torque exerted on the wheels to be the greatest then?

That's what is interesting about the problem. It is not immediately obvious where that will be.
Draw the diagram as I described. Which force results in torque?

 

[ballboy]

Ok I'll draw it but I don't know where you want me to put the ball.

 

[haruspex]

Ok I'll draw it but I don't know where you want me to put the ball.

The ball is partly squeezed. It is not yet directly between the wheels.

 

[ballboy]

OK this is where is just enters

 

[haruspex]

OK this is where is just enters

But I said "partly squeezed". You don't want any special point, such as just about to be squeezed or maximally squeezed; you want a generic situation somewhere between the two. Please label the diagram, not necessarily using the labels I defined, but assigning some label to each of the five points I mentioned. Might help to set angles ABE and BAD as θ.

 

[ballboy]

But I do have ABCDE labelled in the picture. Did you not see them?

 

[haruspex]

But I do have ABCDE labelled in the picture. Did you not see them?

Yes, that's fine, but do the same with the generic picture. And don't forget the frictional forces.

 

[ballboy]

Ok here's the ball partly in. I don't know what you mean about frictional forces. What are they and how do I show them?

 

[haruspex]

Ok here's the ball partly in. I don't know what you mean about frictional forces. What are they and how do I show them?

Consider the forces on the ball. Remember that if the wheels stop it should be in equilibrium in this position.

 

[ballboy]

But the wheels never stop. These ball machines propel them forward at anywhere from 20-80mph depending on the wheel rpm.

I don't know what forces are on the ball except the wheel pressing.

 

[haruspex]

But the wheels never stop.

No, but if they were to stop you would expect the ball to stay where it is, so the forces must be in equilibrium.

I don't know what forces are on the ball except the wheel pressing.

Which direction are the wheels pressing in?

 

[ballboy]

The wheels aren't really pressing. They are always in the same place but rotating. If the wheels moved the ball would not propel. The ball gets squeezed so there is an equal and opposite reaction on the wheels I figure. That force results in torque on the wheel I think. The ball going through the wheels has to slow down the wheels by creating a force and that's what I am trying to figure out.

 

[haruspex]

The wheels aren't really pressing.

Of course they are. How else does the ball get squeezed?
What forces are there in general between two circular shapes in contact? Which directions do those forces point in?
If the ball is in equilibrium as a result, what can you say about the resultant of the forces from one wheel?

 

[scottdave]

But the wheels never stop. These ball machines propel them forward at anywhere from 20-80mph depending on the wheel rpm.

I don't know what forces are on the ball except the wheel pressing.

What forces cause the ball to get sucked into the narrow gap? What is the force when 2 surfaces rub against each other?

 

[ballboy]

The rubber wheels kind of 'grip' the ball as it gets thrown in between the wheels after it falls down by gravity through the angled chute that drops down from the ball hopper with all the balls in it. When I say not pressing I mean the wheels are not moving in any direction except rotating. They are fixed.

I think the forces from the ball are pointing towards the origin of the wheel, ie the centre point of each wheel axle as it moves between the wheels.

I have no clue what the answer is to your last question. Its not really in equilibrium as a result because the ball keeps moving.

 

[ballboy]

What forces cause the ball to get sucked into the narrow gap? What is the force when 2 surfaces rub against each other?

The ball following down the chute from the ball hopper and having some momentum.

I don't know the answer to your second question. I guess just the opposing force from the ball, ie the amount of force required to squeeze it.

 

[haruspex]

Its not really in equilibrium as a result because the ball keeps moving.

An object on which the forces are in equilibrium can nevertheless move at constant velocity. In reality, it may be accelerating, but we can imagine slowing it down to the point where the acceleration is negligible. The forces must be very nearly in equilibrium.

I think the forces from the ball are pointing towards the origin of the wheel,

By action and reaction, what direction is the force from the wheel on the ball? If both wheels are exerting that radial (from their perspective) force on the ball, and nothing else, which way will the ball go?

 

[ballboy]

An object on which the forces are in equilibrium can nevertheless move at constant velocity. In reality, it may be accelerating, but we can imagine slowing it down to the point where the acceleration is negligible. The forces must be very nearly in equilibrium.

By action and reaction, what direction is the force from the wheel on the ball? If both wheels are exerting that radial (from their perspective) force on the ball, and nothing else, which way will the ball go?

I would think the force is in 2 directions, both towards the center of the ball and tangential to the circumference.

 

[scottdave]

The rubber wheels kind of 'grip' the ball as it gets thrown in between the wheels after it falls down by gravity...

Ok, so the surface of the spinning wheels grip the ball. I would call the force due to friction. What direction does frictional forces act in?

 

[ballboy]

Tangential to the circumference (ie edge) of the ball where it makes contact with the wheels.

 

[haruspex]

I would think the force is in 2 directions, both towards the center of the ball and tangential to the circumference.

Yes, but more to the point, radial and tangential to the wheel.
Which of those requires torque from the wheel?

 

[ballboy]

Radial I think or the wheel could not propel the ball. What I am trying to figure out is how much the wheels slow down because that ball is going between them.

 

[haruspex]

Radial I think or the wheel could not propel the ball.

No. A force radial to the wheel has no torque about its centre. The magnitude of the torque of a force about an axis is the magnitude of the force multiplied by the perpendicular distance from the axis to the line of action of the force. If the force is radial that perpendicular distance is zero.
What does that leave?