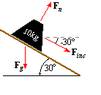
Force normal and force along the incline

  • Context: MHB 
  • Thread starter Thread starter WMDhamnekar
  • Start date Start date
  • Tags Tags
    Force Incline Normal
Click For Summary

Discussion Overview

The discussion revolves around calculating the force components acting on a block resting on an inclined plane, specifically the force along the incline ($F_{inc}$) and the normal force ($F_n$). Participants explore the decomposition of gravitational force into orthogonal components and the relationships between these forces in the context of a 30-degree incline.

Discussion Character

  • Technical explanation
  • Mathematical reasoning
  • Debate/contested

Main Points Raised

  • One participant states that gravitational force ($F_g$) can be decomposed into two orthogonal vectors, leading to the equation $F_g = F_{inc} - F_n$.
  • Another participant suggests that $F_g$ is -98N and proposes a calculation for $F_{inc}$ using the expression $F \langle \cos{60^\circ}, \sin{60^\circ} \rangle$.
  • Several participants discuss the geometry of the situation, referencing a 30-60-90 triangle where $F_g$ is the hypotenuse and $F_{inc}$ and $F_n$ are the legs.
  • There is a proposal to use sine functions to express $a$ and $b$ in terms of $F_g$, with $a = F_g \sin(30)$ and $b = F_g \sin(60)$.
  • One participant claims to have calculated $F_{normal}$ as 84.957N and $F_{inc}$ as 49N, based on their diagram and the relationships derived from the triangle.
  • Another participant confirms the calculated values and provides a reasoning based on the angles formed between the forces and the gravitational force.

Areas of Agreement / Disagreement

Participants express varying methods and interpretations for calculating the forces, with some agreeing on the numerical values while others question the approach and the need for diagrams to clarify the relationships. No consensus is reached on a single method or interpretation.

Contextual Notes

There are unresolved aspects regarding the definitions of the forces and the assumptions made in the calculations, particularly concerning the angles and the signs of the components. The discussion also reflects differing interpretations of the geometric relationships involved.

WMDhamnekar
MHB
Messages
381
Reaction score
30
A 10 kg block sits on a board inclined to an angle of $30^\circ$ with the horizontal.

What are $F_{inc}$ (force along the incline) and the $F_n$ (force normal)?How to compute this?
 

Attachments

  • inclined.gif
    inclined.gif
    982 bytes · Views: 132
Physics news on Phys.org
You are decomposing $${F}_{g}$$ into 2 orthogonal vectors so

$${F}_{g} = {F}_{inc} - {F}_{n}$$
 
DavidCampen said:
You are decomposing $${F}_{g}$$ into 2 orthogonal vectors so

$${F}_{g} = {F}_{inc} - {F}_{n}$$
Hello,

Here $F_g=-98N$. What is $F_{inc}?$ I think it is $F\langle \cos{60^\circ},\sin{60^\circ}\rangle$ What is $F_{normal}?$

They should be orthogonal to each other means their dot product =0.
 
The 2 component vectors will be at right angles to one another. One will have an angle of 30 degree to ${F}_{g}$ and the other 60 degrees.

So think of a 30-60-90 right triangle with ${F}_{g}$ the hypotenuse and ${F}_{inc}$ and ${F}_{n}$ the legs.
 
Last edited:
DavidCampen said:
The 2 component vectors will be at right angles to one another. One will have an angle of 30 degree to $${F}_{g}$$ and the other 60 degrees. So $$asin(30) + bsin(60) = {F}_{g}$$. Which of a and b is $${F}_{inc}$$ and which is $${F}_{n}$$ (and the correct sign) you will have to draw a diagram to figure out.

Hello,

$a\sin{30^\circ}$ is + $F_n$ and $b\sin{60^\circ}$ is $-F_{inc}$. How to compute a and b? Would you explain with a graph?
 
Yes, excuse me.

$a = {F}_{g}sin(30)$ and $b = {F}_{g}sin(60)$

I edited my post just above to match this.
 
DavidCampen said:
Yes, excuse me.

$a = {F}_{g}sin(30)$ and $b = {F}_{g}sin(60)$

I edited my post just above to match this.

So, the $F_{normal}=84.957N$ and $F_{inc}=49N$
 
Dhamnekar Winod said:
So, the $F_{normal}=84.957N$ and $F_{inc}=49N$
Yes.

I drew a diagram. Placing ${F}_{inc}$ on the horizontal axis as one leg of the triangle, ${F}_{n}$ as the vertical leg and ${F}_{g}$ as the hypotenuse I get an angle of 60 deg. between ${F}_{inc}$ and ${F}_{g}$ so the magnitude of ${F}_{inc}$ = ${F}_{g} cos(60) = 0.5 {F}_{g}$ and ${F}_{n} = {F}_{g}sin(60) = 0.87{F}_{g}$.
 
Last edited:

Similar threads

MHB What Tension is Required for a 10 kg Mass to Hang Motionless?
  • · Replies 7 ·
Replies
7
Views
1K
Undergrad Reaction force of and its relation to normal force and friction
  • · Replies 20 ·
Replies
20
Views
4K
Static equilibrium | Uniform sphere on incline | Determining friction
  • · Replies 43 ·
2
Replies
43
Views
2K
High School Normal Force Discrepancy for Wedge Vs. Ramp
  • · Replies 9 ·
Replies
9
Views
3K
High School Determine forces acting on double inclined plane
  • · Replies 13 ·
Replies
13
Views
2K
High School Normal force in case of inclined plane and banked turn
  • · Replies 3 ·
Replies
3
Views
2K
High School Beam on an inclined plane
  • · Replies 4 ·
Replies
4
Views
698
Block tied to a fixed string on an accelerating wedge
  • · Replies 37 ·
2
Replies
37
Views
3K
Undergrad How does a screw roll down an inclined plane?
  • · Replies 5 ·
Replies
5
Views
3K
Block and pulley on movable incline
  • · Replies 2 ·
Replies
2
Views
2K