Force of friction in turning cars

[ChessEnthusiast]

I read an article where the author tried to find the maximal speed a car can have when taking a turn of certain radius. They represented the car as a point and claimed that the force of friction is the centripetal force - acting perpendicular to the trajectory of the car.

I do understand why friction is the force that propels the car. What I don't understand is: Why is the net force acting on a car perpendicular to its trajectory?

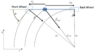
I have drawn this diagram:
The rectangle is the car.
The green segments are the wheels.

What is wrong with my diagram?

 

[Orodruin]

You seem to be under the (faulty) impression that friction can only act in the direction of the wheels. This is not the case. If the wheels roll without resistance (idealisation), the least friction force will be needed when the car turns at constant speed. If this is the case, then
$$
\frac{dv^2}{dt} = 2\vec v \cdot \vec a = 0,$$
ie, acceleration is then perpendicular to velocity.

 

[willem2]

What is wrong with my diagram?

Your direction of friction doesn't make sense.
As long as the wheels are rolling and not slipping, the sideways component of friction is just whatever is needed to make the wheel go straight ahead.
The friction force in the forward direction is just (force from the engine) - (braking force) - (rolling friction). In most cases this should be close to 0, as you should neither brake nor step on the gas while cornering, so the friction force tends to be only sideways.

Note that when you start cornering, there will only be a sideways force on the front wheels, but as the car turns round, and the direction that the car moves starts to differ from the direction where the back wheels are pointing, you'll get a sideways friction force from the back wheels as well.
While you are in a curve, the car is rotating at constant speed, and the torques from the forces from the front and from the back wheels will have to cancel, or the car will be spinning out of control.

 

[tnich]

You are probably familiar with the spherical cow joke. Here it seems you are dealing with a spherical car. Apparently, the author of the article has assumed that tangential forces of friction and air resistance are negligible, and that may or may not be a justifiable assumption.

Why is the net force acting on a car perpendicular to its trajectory?

If the car moves at constant speed as it travels a circular arc, then its tangential acceleration is zero. So all of the acceleration (and hence the net force) is perpendicular to its trajectory.

What is wrong with my diagram?

If you want to deal explicitly with the tangential forces, you will need show them all in your diagram. They would need to include at the least a frictional force in the forward direction on the back wheels, and a frictional force in the backward direction on the front wheels due to the fact that they are turned at an angle to the direction of travel. If you assume those are the only tangential forces, then they cancel and the net frictional force is perpendicular to the trajectory.

As @willem2 points out, there is also a perpendicular friction force on the back wheels.

The center of gravity of the car will come into play. Depending on the vehicle speed, air resistance may also be significant. You could even consider the friction of the wheels turning on their axels.

Where does it end? The author has made some assumptions and told you what they are. You always have the option of solving the problem under different assumptions.

 

[ChessEnthusiast]

What if the car were accelerating when cornering, had all-wheel drive and only front wheels could turn?

Would my diagram then be correct?

@tnich
I don't understand why the fact that the wheels are turned at an angle causes them to experience backward-friction. Could you give me some hints why it's the case?

 

[A.T.]

What if ...

Are you trying to understand how cars actually turn or to construct some unlikely hypothetical situation?

 

[ChessEnthusiast]

@A.T.
Is the situation I've described unlikely hypothetical?
The direction of friction in turning cars keeps puzzling me - I'm trying to finally comprehend it.

 

[A.T.]

@A.T.
Is the situation I've described unlikely hypothetical?

Eliminating all lateral forces on all wheels is not what usually happens during a turn on level ground.

 

[ChessEnthusiast]

@A.T.
In my opinion, only the front wheels will experience a lateral force - the horizontal component of the force of friction.
Once the car has turned a bit, the rear wheels will also experience sideways component of friction.

Have I ommitted any important forces?

 

[Orodruin]

What if the car were accelerating when cornering, had all-wheel drive and only front wheels could turn?

Would my diagram then be correct?

No. It has nothing to do with reality in any reasonable situation. I suggest reading and trying to understand the answers you have been given and if necessary asking questions about them rather than trying to press your square box through the round hole.

 

[A.T.]

Have I ommitted any important forces?

Yes, the lateral friction forces on the wheels, where "lateral" means parallel to the wheel spin axis.

 

[lomidrevo]

@ChessEnthusiast , maybe realizing what happens during the two extreme situations could improve your understanding:
1) when the wheels are straight (aligned parallel to the direction of motion), there is no friction force acting from left or right - i.e. car is continuing without turning
2) when the wheels are turned at right angle (aligned perpendicular to the direction of motion), there is friction force exactly opposite to the direction of motion of the car, which slows down and eventually stops the car. Not recommended to do this at high speeds :)
3) finally turning the wheels at some angle just between the two extremities, will result in a friction force that will provide the desired centripetal acceleration allowing you to turn the car. Keep in mind that the friction force is parallel to the wheel spin, as already mentioned by @A.T. The angle you use for turning the wheels directly implies the direction of the centripetal acceleration.

 

[FactChecker]

@A.T.
In my opinion, only the front wheels will experience a lateral force - the horizontal component of the force of friction.
Once the car has turned a bit, the rear wheels will also experience sideways component of friction.

Have I ommitted any important forces?

You have omitted the lateral force of the rear tires. If the car is going in a circle, the rear of the car would want to go streight and would want to "spin out". The only thing stopping that is the lateral force of the rear tires.

PS. In the larger scope, keep in mind that the only way that an object can travel in a perfect circle is for its acceleration (and therefore the net force) to always be pointed directly toward the center of the circle. That is always at a right angle to the velocity vector of the object. So that is a given. Whether the car is pointing exactly in the direction of its velocity vector or not is another question, but we can assume that it is a close approximation.

 

[Mister T]

What is wrong with my diagram?

For uniform circular motion you need a net force towards the center of the circle. Note that you could achieve this by altering only the magnitudes of the forces in your diagram. Whether that represents a reasonable physical situation or not, I'm not sure. I'd have to think about it some more.

 

[tnich]

Here is a fully worked-out solution.

Assumptions:
1) The system can be well-approximated as a rod with a wheel on each end.
2) The only forces considered are frictional forces. Air resistance and all other forces are ignored. This assumption could result in significant error if the car is moving at high speed.
3) The system in steady state, turning at a constant speed on a circular arc.
4) The wheels do not slip.

Constant speed and constant turn radius imply that angular momentum is constant and net torque is zero, resulting in
$0 = \vec r_f \times \vec F + \vec r_B \times \vec B$
$0 = |\vec r_F|~F_y + |\vec r_B|~B_y~~~1)$

Constant speed implies that tangential acceleration is zero, so the net force is perpendicular to the velocity vector

$\vec F_{net} = \vec F + \vec B$
$0 = F_x + B_x$
$F_{net} \equiv |\vec F_{net}| = -(F_y + B_y)~~~2)$

Solving 1) and 2) for $B_y$ and $F_y$ gives us

$B_y = -\frac {|r_F|} {|r_F| + |r_B|} F_{net}$
$F_y = -\frac {|r_B|} {|r_F| + |r_B|} F_{net}~~~3)$

which shows that there is a lateral frictional force on the rear wheel.

Since the front wheel rolls at a constant speed without slipping, the frictional force on the wheel must be along its axis. Now here is the tricky part. The net force on the wheel is perpendicular to $\vec v$, which is not the same direction. How can the tire not slip in that case? The tire deforms to allow it to travel in a different direction than it is rolling.

Given that $\vec F$ is along the wheel axis,

$F_y = -|\vec F| \cos \theta ~~~4)$

Combining 3) and 4), we get

$F \equiv |\vec F| = \frac {|r_B|F_{net}} {(|r_F| + |r_B|)\cos \theta} = \frac {|r_B|m~a_{rad}} {(|r_F| + |r_B|)\cos \theta}$

the magnitude of the frictional force on the front wheel as a function of the radial acceleration $a_{rad}$.

 

[tnich]

Since the front wheel rolls at a constant speed without slipping, the frictional force on the wheel must be along its axis. Now here is the tricky part. The net force on the wheel is perpendicular to $\vec v$, which is not the same direction. How can the tire not slip in that case? The tire deforms to allow it to travel in a different direction than it is rolling.

This has bothered my since I posted it. In thinking about it, I discovered an incorrect assumption in my previous post. The net force is not perpendicular to the body of the car at the center of mass. It is perpendicular at the back wheel. The front and back wheels and the center of mass all revolve around a common center, but at different radii. To justify this new assumption, consider that the back wheel simply moves toward the current position of the front wheel, independent of which direction the front wheel is pointing.

From this we can see that
$d_F = \frac {|r_F| + |r_B|} {\sin \alpha}$
$d_B = \frac {|r_F| + |r_B|} {\tan \alpha}$
$d_{CM} = \sqrt {|r_B|^2 + \left (\frac {|r_F| + |r_B|} {\tan \alpha}\right )^2}$

and
$F_{net} = m \omega^2 \sqrt {|r_B|^2 + \left (\frac {|r_F| + |r_B|} {\tan \alpha}\right )^2}$

where $\omega$ is the angular velocity.

The equations
$0 = \vec r_f \times \vec F + \vec r_B \times \vec B$ and
$\vec F_{net} = \vec F + \vec B$

still hold, but now instead of
$0 = F_x + B_x$

we have
$0 = B_x$

solving these equations results in
$F = \frac {|r_B|m~a_{rad}} {(|r_F| + |r_B|)} = \frac {m\omega^2 |r_B|}{\sin \alpha}$

The difference between this and my previous solution is the lack of $\cos \theta$ in the denominator of the expression for $F$. The front wheels and the back wheels travel in the directions they are rolling, eliminating the need for an uncomfortable explanation of why they don't. This solution also eliminates the need for friction acting in the $x$-direction on the back wheel.

 

[rcgldr]

I'm thinking the original post is correct, that the net force is perpendicular to the trajectory (path of the CM) of the car. If there was a net force component parallel to the path (tangential force), then the car would be increasing or decreasing speed.

 

[tnich]

I'm thinking the original post is correct, that the net force is perpendicular to the trajectory (path of the CM) of the car. If there was a net force component parallel to the path (tangential force), then the car would be increasing or decreasing speed.

Sounds like we are in agreement.