- #1
alkaspeltzar
- 354
- 37
- TL;DR Summary
- I understand for a car to turn, there must be a centripetal force. As the car turns it is friction of the front wheels creates an inward force. How, looking for a conceptual answer
Hello, as you can see i am trying to understand conceptually how the tires during turning create a centripetal force. It was explained to me that as we turn the car tires, the tires similar to a ski or a wedge, now want to push the ground to the side and forward. If the ground was loose, this makes sense as the tires would slide forward and scrap the ground to the side. Is it this force of friction that causes the ground to push back, have a perpendicular component, pushing the car inward and turn?
As you negotiate a turn, if you are turning left, your wheels are pushing to the right against the floor. Static friction allows the floor to "push back" against your wheels, allowing you to turn left.
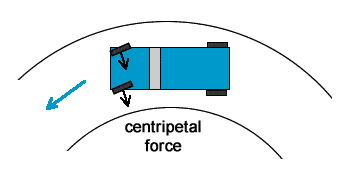
As you negotiate a turn, if you are turning left, your wheels are pushing to the right against the floor. Static friction allows the floor to "push back" against your wheels, allowing you to turn left.