kekpillangok
- 15
- 2
- Homework Statement
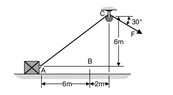
- In the figure below, a constant force F pulls the string at an angle of 30° with the horizontal. At the other end of the string, a 10 kg block is attached, which starts from rest at point A and reaches point B with a speed of 6 m/s. Neglect all friction and the mass of the pulley. Find the approximate value of the force F.
OPTIONS: 50 N, 100 N, 150 N, 200 N, 250 N
- Relevant Equations
- F = ma
W = delta_KE
I can't understand what is going on here. My intuition tells me that the traction pulling on the block should be equal to F. Apparently, however, the problem would have me believe that this is not the case, as it gives me a 30° angle at which the force acts and a 6-8-10 triangle as ways to decompose the force acting on the block. I don't understand why the force should not be the same throughout the string. Isn't this a necessary condition for the string to work at all? Shouldn't the tension on it be the same throughout?
Here's what I've tried. Assuming ##F ## is the same force acting directly on the block, I reasoned that its horizontal component did positive work on the block and increased its kinetic energy to 180 J, so, from the 6-8-10 triangle: $$F \cdot \frac{4 }{5 }\cdot 6 =\frac{1 }{2 }\cdot 10 \cdot 36 $$.
Solving for F gives F = 37.5 N, which is not an option.
I then imagined that, perhaps, the force that acted on the block was the horizontal component of F—that is, ##F \cdot \frac{\sqrt{3 }}{2 } ##, from the 30° angle. I then wrote ##F \cdot \frac{\sqrt{3 }}{2 }\cdot 6 =\frac{1 }{2 }\cdot 10 \cdot 36 ##, which gave me ##F \approx 43.3 ##N, which doesn't look right either. I also tried considering the vertical component of the force acting on the block as the vertical component of F, and obtaining the horizontal component from the 6/8 ratio on the triangle, but this also did not work. At any rate, this is just trial and error at this point.
It makes sense to me that there should be a difference in the force acting on the block depending on whether you pull right down on the string or at an angle, but I can't quite concile this with what I previously learnt about strings, in particular that the force throughout the string should be the same. If anyone can help me understand this new situation, I will be very grateful.
Here's what I've tried. Assuming ##F ## is the same force acting directly on the block, I reasoned that its horizontal component did positive work on the block and increased its kinetic energy to 180 J, so, from the 6-8-10 triangle: $$F \cdot \frac{4 }{5 }\cdot 6 =\frac{1 }{2 }\cdot 10 \cdot 36 $$.
Solving for F gives F = 37.5 N, which is not an option.
I then imagined that, perhaps, the force that acted on the block was the horizontal component of F—that is, ##F \cdot \frac{\sqrt{3 }}{2 } ##, from the 30° angle. I then wrote ##F \cdot \frac{\sqrt{3 }}{2 }\cdot 6 =\frac{1 }{2 }\cdot 10 \cdot 36 ##, which gave me ##F \approx 43.3 ##N, which doesn't look right either. I also tried considering the vertical component of the force acting on the block as the vertical component of F, and obtaining the horizontal component from the 6/8 ratio on the triangle, but this also did not work. At any rate, this is just trial and error at this point.
It makes sense to me that there should be a difference in the force acting on the block depending on whether you pull right down on the string or at an angle, but I can't quite concile this with what I previously learnt about strings, in particular that the force throughout the string should be the same. If anyone can help me understand this new situation, I will be very grateful.