- #1
paulimerci
- 287
- 47
- Homework Statement
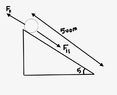
- A biker and his bike have a combined mass of 90kg. The rider starts from rest and rolls(no pedalling) down an incline that is 500m long. The plane is at an incline of 5 degrees above the horizontal. The average frictional force acting on the bike/rider is equal to 60N. Find the speed of the biker at the bottom of the hill.
- Relevant Equations
- Net work done on a system = change in K.E
I used the work-energy equation to solve this problem.Only the parallel component of force acts to accelerate the biker and increases K.E., so only the parallel component and frictional force does work on the biker.
therefore,
Net work done on a system = change in K.E
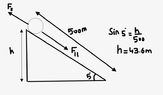
$$(F_I{_I} + F_F) d cos\theta = \frac{1}{2} m\cdot v_f^2$$
$$ (mg sin\theta \cdot d cos\theta) + (F_F d cos\theta) = \frac{1}{2} m\cdot v_f^2$$
$$ (90 \cdot 10 \cdot sin 5 \cdot 500 \cdot cos0) + (60 \cdot 500 \cdot cos 180) = \frac{1}{2} m\cdot v_f^2$$
$$ v_f = 14.31 \frac{m}{s}$$
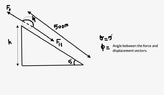
where, ##cos 0## - angle between the force and the displacement, where the parallel component of force is in the direction of motion and ##cos180## - angle between the frictional force and the displacement, ##v_i =0##
I know something is not right in the above equations that I solved. I didn't include GPE which should give me a different set of equations, and I didn’t use that approach; I'm just confused. Any help would be greatly appreciated.
therefore,
Net work done on a system = change in K.E
$$(F_I{_I} + F_F) d cos\theta = \frac{1}{2} m\cdot v_f^2$$
$$ (mg sin\theta \cdot d cos\theta) + (F_F d cos\theta) = \frac{1}{2} m\cdot v_f^2$$
$$ (90 \cdot 10 \cdot sin 5 \cdot 500 \cdot cos0) + (60 \cdot 500 \cdot cos 180) = \frac{1}{2} m\cdot v_f^2$$
$$ v_f = 14.31 \frac{m}{s}$$
where, ##cos 0## - angle between the force and the displacement, where the parallel component of force is in the direction of motion and ##cos180## - angle between the frictional force and the displacement, ##v_i =0##
I know something is not right in the above equations that I solved. I didn't include GPE which should give me a different set of equations, and I didn’t use that approach; I'm just confused. Any help would be greatly appreciated.