Force vs. Displacement graph question

[Plasm47]

In the graph below, forces labelled positive act in the direction of motion of the object, forces labelled negative oppose the motion. The object under consideration has a mass of 2.0kg and was initially at rest. Calculate its kinetic energy and speed when
a) d= 2.0m
b) d= 4.0m
c) d=6.0m
d) d= 8.0m

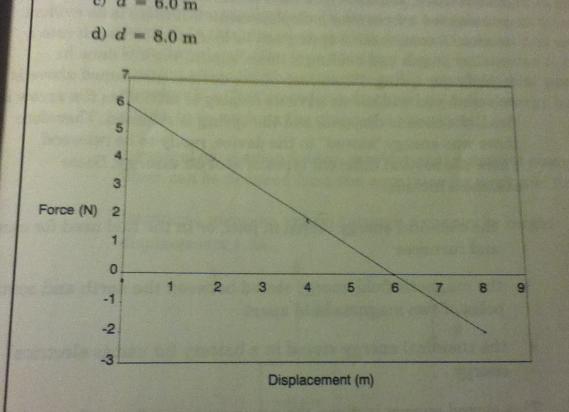
I know W is area under the graph, but not positive how to apply it. I assume the question is only asking for that moment in time, and NOT a time period.
so for (a) it would be W= 4.0N x 2.0m = 8J; which would also be E_k
and V= 2.83m/s
if this is correct then b and c follow the same method, so i got those right aswell.
Not sure of the procedure when the Force is negative.

 

[nasu]

No, this is not right. The kinetic energy at a given moment is equal to the work done from the beginning to that moment - given that it starts from rest so in the beginning has zero KE.
The work done can be calculated form the area under the curve, as you said (but did not do).

 

[Plasm47]

No, this is not right. The kinetic energy at a given moment is equal to the work done from the beginning to that moment - given that it starts from rest so in the beginning has zero KE.
The work done can be calculated form the area under the curve, as you said (but did not do).

okay, in that case:
a)to calculate work, solve for area under curve
W= l x w + (bXh)/2
W= 2m x 4N + (2m x (6N-4N)/2
W= 8J + 2J
w= 10 J
The E_k is equivilant to w since there is no work lost in the process.
E_k= 10J

now, solve for velocity
E_k= 0.5 (m)v²
v²= 0.5(2.0kg)/10J
v²= 0.1
v= √0.1
v=0.3m/s (to two sig digs)

if this is correct, then (b), (c), and (d) follow the same process

 

[nasu]

The value of the work looks OK.
Solving for v is not done properly (you can convince yourself calculating the KE with v=0.3m/s and m=2 kg).
Look again at the equation to solve.