Forces that act on a physical pendulum

[Yossi33]

Homework Statement

physical pendulum

Relevant Equations

torque=Ia

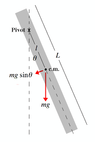
hello, i have a question about the forces that act on a rod at it's pivot point. the rod is free to rotate about the pivot point at the edge and it starts from rest parallel to the ground.the question is : when it reach to angle theta find the a] the angular velocity b] angular acceleration c] the forces acts on the rod at the pivot point (normal)
the rod is of length L and mass M
i found w^2=(3gcos(theta))/L
angular acceleration=alpha=(3gsin(theta))/2L
c- i try to calculate the normal force that acts toward the pivot point
N-mgcos(theta)=Mw^2R
and R=L/2. but it's not the answer and i searched at the interent and find that there are 2 forces act at the pivot point of the rod and i didn't understand why. thanks for the help.

 

[haruspex]

Homework Statement:: physical pendulum
Relevant Equations:: torque=Ia

there are 2 forces act at the pivot point of the rod and i didn't understand why

If the force from the pivot were only along the line of the rod then both forces (that and gravity) would have lines of action through the rod’s mass centre. So there would be no torque to create the angular acceleration.

 

[Yossi33]

so what are the forces that act there, what are their direction?
and mgsin(theta) is a component of the gravity that perpendicular to the radius of rotation this force does the torque , no?

 

[haruspex]

so what are the forces that act there, what are their direction?
and mgsin(theta) is a component of the gravity that perpendicular to the radius of rotation this force does the torque , no?

The tangential component of gravity exerts a torque about the pivot, but not about the mass centre.
You can express the angular acceleration of the rod in terms of that torque about the pivot, or by the torque the forces at the pivot exert about the mass centre. Since the angular acceleration is the same either way, you can find the relationship between the gravitational force and the component of the pivot force normal to the rod.

 

[Yossi33]

thank you for your help.
i think i understood what you meant and tried to get the relation in this photo

 

[haruspex]

thank you for your help.
i think i understood what you meant and tried to get the relation in this photoView attachment 295316

Well done.

 

[Yossi33]

thanks man,please if you can still help me to fully understand it, because i don't understand why there has to be 2 forces .
can i treat it as a normal force that opposite the wiegh components?
and because there is a torque in the tangential axis , i can't calculate the forces only with Newtons second law?
mgsin(theta)-Fn(tangential)=ma(tangential)
or this is another way
?

 

[haruspex]

thanks man,please if you can still help me to fully understand it, because i don't understand why there has to be 2 forces .
can i treat it as a normal force that opposite the wiegh components?

It's not that there are two forces. The reaction from the pivot is one force, but you can opt to resolve it into two perpendicular forces in any way you choose.
If you resolve it into one component along the rod and one normal to it then both are nonzero.

can i treat it as a normal force that opposite the wiegh components?

Not sure what you mean.

because there is a torque in the tangential axis , i can't calculate the forces only with Newtons second law?

Torques have no relevance to $\Sigma F=ma$.

mgsin(theta)-Fn(tangential)=ma(tangential)

That's correct, if by Fn(tangential) you mean the component normal to the rod of the reaction force at the pivot.