Formulation rigid body constraint

[Larsen1000]

Hello

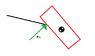
I need some help with formulating the constraint force for a sliding and rotating box. The scenario is: A box is sliding down a slanted table. The center of gravity has passed the edge of the table so the box receives a counter force and torque.

I am solving the forces and moments which acts through center of gravity and therefore have formulated:

F_n = -(gravity * Rotation matrix *Constraint vector) - (Forces from external moments and rotational velocity)

The constraint vector is [0 1] which eliminates tangent forces at the edge and leaves the normal force. The point where I have problems is to formulate the constraint force caused by the rotational component. Can someone help me with this?

 

[K^2]

Are you trying to approach this from Lagrangian formalism or Newtonian formalism? For the later, you don't need the angular component. Just solve for normal force that gives normal acceleration = 0, and then substitute that along with point of contact for torque. The force will depend on angle, but not on angular velocity.

For Lagrangian formalism, you only need the constraint equation. Easiest way to get that is to take coordinate of the CoM to be (x,y) and of the contact point (0,0). Then you trivially get ycosθ-xsinθ=h/2 as your constraint equation, where h is the height of the brick and θ corresponds to brick laying flat on horizontal surface.

Of course, you need to keep in mind that at some point the brick will separate. Watch for F_n changing sign.