Fourier Series Convergence for Square Wave Function

[izen]

Homework Statement

what values does the Fourier series for f(t) converge to if t = 0 and t = 2?

Homework Equations

The Attempt at a Solution

My answers the red rectangles for the even function t=0 >> 1 and t=2 -->1.5
and odd function t=0 >> 0 and t=2 -->1.5
because at t=0 is continuity so the value is = f(t) but at t=2 is discontinuity so the value is average of the 2 functions.

but my answers is wrong the even function t=0 >> 1 and t=2 -->2
and odd function t=0 >> 0 and t=2 -->2

why is that ? please give some feedback thanks

 

[collinsmark]

Hello Izen,

The question, as it seems to be written, is kind of weird. You might have to reconsider what the question is really asking.

For part a), you have correctly sketched an "even" function. But it's not periodic. Notice that around t = 0 there are two adjacent segments where f_e(t) = 1; this doesn't occur anywhere else in the waveform, meaning the way you have sketched it, the function is aperiodic. The Fourier series only applies to periodic functions. So if this question is about Fourier series, you'll have to rethink it. (Hint: try making the first rise up to f_e(t) = 2 happen at t = +/- 1/2.)

For part e), you have correctly sketched an "odd" function. But it's not periodic. Here is where the question is really weird though; you won't be able make a truly odd function such that the Fourier series applies. So the question is a little weird (maybe misleading?) in this way. I'm guessing the question wants you take the waveform from part a) and just shift it to the right or left by 1/2. It's not truly an "odd" function that way, but if the Fourier series is to apply, it must be periodic.

 

[collinsmark]

On further thought, in part a), the question *might* be asking you to sketch a waveform that has two segments of f_e(t) = 1 followed by one segment of f_e(t) = 2, followed by another two segments of f_e(t) = 1, followed by one segment of f_e(t) = 2, and so on. [With f_e(0) being right in the middle of two segments where f_e(t) = 1.]

For part e) the question *might* be asking you to sketch a waveform that has one segment of f_o(t) = 1 followed by one segment of f_o(t) = 2, followed by one segment of f_o(t) = -2 followed by one segment of f_o(t) = -1, with everything repeating after that.

Doing it this way is the only way to do it such that the question is self-consistent. I suggest doing it this way, instead of what I suggested in my previous post.

 

[rude man]

Definition: "odd extension" means f(-x) = - f(x). You drew this extended function correctly.
Call ext.f(x) as the extended f(x).

So your f(x) = 1, 0 =< x < 1 and f(x) = 2, 1 < x <= 2. Notice that f(x) = 2 at x = 2. This is critical. Your f(x) is defined at x = +2. It is not defined for x > 2 and so there is no jump at x = 2.

And the ext.f(x) is -2, -2 < x < -1 and -1, -1 < x < 0 with jumps at x = -1 and x = 0 and with no change from x = 0 to x = +2.
So at x = 0 you jump from -1 to +1 so the convergence is x = 0.

Again, nothing has changed for your extended function for x => 0. So f converges to the actual unextended function which at x = 2 is f = 2 as you're given.

Definition: "Even extension" means f(-x) = - f(x). You have also drawn this ext.f(x) correctly.

Can you do the same thing now to even-extended f(x)?
At x = 0 it's obviously what you wrote. But again, what is ext.f(x) at x = +2?

 

[izen]

Definition: "odd extension" means f(-x) = - f(x). You drew this extended function correctly.
Call ext.f(x) as the extended f(x).

So your f(x) = 1, 0 =< x < 1 and f(x) = 2, 1 < x <= 2. Notice that f(x) = 2 at x = 2. This is critical. Your f(x) is defined at x = +2. It is not defined for x > 2 and so there is no jump at x = 2.

And the ext.f(x) is -2, -2 < x < -1 and -1, -1 < x < 0 with jumps at x = -1 and x = 0 and with no change from x = 0 to x = +2.
So at x = 0 you jump from -1 to +1 so the convergence is x = 0.

Again, nothing has changed for your extended function for x => 0. So f converges to the actual unextended function which at x = 2 is f = 2 as you're given.

Definition: "Even extension" means f(-x) = - f(x). You have also drawn this ext.f(x) correctly.

Can you do the same thing now to even-extended f(x)?
At x = 0 it's obviously what you wrote. But again, what is ext.f(x) at x = +2?

I still cannot see it where it is defined f(x) = 1, 0 =< x < 1 and f(x) = 2, 1 < x <= 2. What I see on the question is f(x) = 1, 0 < x < 1 and f(x) = 2, 1 < x < 2.

Maybe I misunderstand something

 

[rude man]

I still cannot see it where it is defined f(x) = 1, 0 =< x < 1 and f(x) = 2, 1 < x <= 2. What I see on the question is f(x) = 1, 0 < x < 1 and f(x) = 2, 1 < x < 2.

Maybe I misunderstand something

Well, you may have written it down without the equal signs at x = 0 and x = 2. Because if x = 2 is not included then the function f is undefined at x = 2 and I don't believe that was the intention. Same goes for x = 0.

Even if x = 2 is not included you have no business drawing a transition from f = 2 back to f = 1 at x = 2!

(If you put a jump in at x = 2 you have violated the rules for function extension).

 

[izen]

Well, you may have written it down without the equal signs at x = 0 and x = 2. Because if x = 2 is not included then the function f is undefined at x = 2 and I don't believe that was the intention. Same goes for x = 0.

Even if x = 2 is not included you have no business drawing a transition from f = 2 back to f = 1 at x = 2!

(If you put a jump in at x = 2 you have violated the rules for function extension).

Hi rudeman, thanks for the reply
yes, I know what you mean but I have checked my book there is no equal signs in that question. and not only this question that has no equal sign most of the questions and examples in my exercise book and lecture note.

 

[rude man]

Hi rudeman, thanks for the reply
yes, I know what you mean but I have checked my book there is no equal signs in that question. and not only this question that has no equal sign most of the questions and examples in my exercise book and lecture note.

Well, I don't see how the book can ask you for convergence of f at a point that does not exist? Probaby we're nitpicking. But you'll have to admit that a transition at x = 2 is not legitimate if we can never get to x = 2.

 

[collinsmark]

There's been a lot of discussion here. But I'll just get to the point. Izen, you *need* to make the function periodic. The Fourier series simply doesn't apply if the function is aperiodic. Also, the problem statement specifically says to plot the *periodic* extensions.

So let's start with the even, periodic extension. You already know what f_e(t) is from 0 < t < 2. Take the mirror image of this (reflected at the y-axis), and plop it down between -2 < t < 0. Now you have an *even* function between -2 < t < 2. Now copy the whole thing between -2 < t < 2 and paste the copy between -6 < t < -2, and another copy between 2 < t < 6. (Keep adding more copies if you want to extend the periodic function out beyond +/- 6.)

Now the odd function. You already know what f_o(t) is from 0 < t < 2. You've also graphed it correctly in your attached photo between -2 < t < 2. (That's one period of the function.) But your graph needs modifications elsewhere. Take exactly what you have between -2 < t < 2, and paste it at -6 < t < -2 and also at 2 < t < 6. If you do it correctly, you should end up with an *odd*, periodic function.

 

[rude man]

There's been a lot of discussion here. But I'll just get to the point. Izen, you *need* to make the function periodic. The Fourier series simply doesn't apply if the function is aperiodic. Also, the problem statement specifically says to plot the *periodic* extensions.

And your response to the convergences at x = 2 is ... ?

 

[collinsmark]

And your response to the convergences at x = 2 is ... ?

I'd say it continues on at f_e(2) = 2.

By the way, I should have given this problem some more thought before posting my earlier responses. If I've contributed to any confusion, I apologize.

 

[collinsmark]

And your response to the convergences at x = 2 is ... ?

I'd say it continues on at f_e(2) = 2.

That's just for the even function though.

For the odd function, f_o(2) is undefined, because the waveform is transitioning from f_o(t) = 2 to f_o(t) = -2, near time t = 2. (And same thing for t = -2.)

 

[rude man]

That's just for the even function though.

For the odd function, f_o(2) is undefined, because the waveform is transitioning from f_o(t) = 2 to f_o(t) = -2, near time t = 2. (And same thing for t = -2.)

How come for the even function convergence is 2 at x = 2 yet for the odd, convergence is "undefined"? It's the same function for x > 0? (And it does not go negative at x = 2!)

 

[collinsmark]

How come for the even function convergence is 2 at x = 2 yet for the odd, convergence is "undefined"? It's the same function for x > 0? (And it does not go negative at x = 2!)

Normally I wouldn't give the original poster this much of the answer. But I feel that we've confused the OP enough that a little further explanation is due. (I am guilty of causing confusion as much as anybody [and I'm probably the biggest offender].) I'll give some additional help on the odd function, and leave the even function details to the OP.

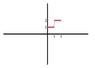
Let's start with the original function:

(I put in a vertical line at t = 1, but you can ignore that without any loss of generality. I'm just "connecting the dots" is all.)

I think we can all agree on that so far.

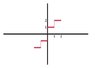
Now we have to make an *odd* function out of this. The OP did it correctly between -2 < t < 2. So I'll just copy that over:

(Again, ignore the vertical, connecting lines, if you wish.)

So far so good.

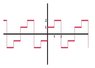
But here is the important point that I intended on making all along (although I might have done a poor job at it): The rest of function must be periodic. We have one period above, and we must extend that same period all the way from negative infinity to infinity. It must be periodic all the way though. (If it isn't periodic, the Fourier series doesn't apply.)

And we then have this:

This is the only way to make a periodic, odd function and still maintain the function's definition at 0 < t < 2.

 

[rude man]

I think we 're having a war of semantics. The definition of extension is to simply reflect the wave about the origin. So anything more negative than for x = -2, or more positive than for x=2, is excluded.

Here is a link explaining that: http://www.math24.net/even-and-odd-...ectly given by the series. It had better be!

 

[izen]

Hi collinsmark & rude man ,
I just found out that my both of my sketches was wrong. It should be the as collinsmark sketch.

Thank you you guys for the comments.