Fourier series equation derivation
- Context: Graduate
- Thread starter merlyn
- Start date
Click For Summary
SUMMARY
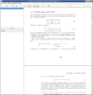
The forum discussion centers on the derivation of equation 21 in the context of exponential Fourier series. Participants emphasize the importance of integrating exponential functions and collapsing products of exponentials into a single term. A worked example is provided, demonstrating the integration of the expression \(\int_0^L e^{i2 \pi nx/L}e^{-i2 \pi mx/L} \, dx\) and simplifying it to \(\int_0^L e^{\frac {i2 \pi(n-m)x} L } \, dx\). The final result includes the term \(\frac{L}{i2 \pi(n-m)} e^{\frac {i2 \pi(n-m)} L x}\).
PREREQUISITES- Understanding of exponential functions and their properties
- Familiarity with integration techniques, particularly definite integrals
- Knowledge of Fourier series concepts, specifically exponential Fourier series
- Basic proficiency in LaTeX for mathematical notation
- Study the properties of exponential functions in the context of Fourier series
- Learn integration techniques for complex exponentials, focusing on \(\int e^{ax} \, dx\)
- Explore additional resources on Fourier transforms and their applications
- Practice using LaTeX for formatting mathematical expressions correctly
Students and educators in mathematics, particularly those focusing on Fourier analysis, as well as anyone seeking to deepen their understanding of exponential functions and integration techniques.
Similar threads
- · Replies 33 ·
- · Replies 23 ·
- · Replies 11 ·
- · Replies 5 ·
Undergrad
Motivation for Fourier series/transform
- · Replies 8 ·
- · Replies 9 ·
- · Replies 7 ·
- · Replies 3 ·
- · Replies 2 ·
Undergrad
Fourier transform of rectangular pulses
- · Replies 5 ·