- #1
PainterGuy
- 940
- 69
- TL;DR Summary
- I have been trying to trace an error in my result without any success. I was trying to compare the application of two different forms of Fourier transform formulae.
Hi,
I tried to apply different forms of Fourier transform, exponential and trigonometric forms, to the same function, f(t)=a⋅e^-(bt)⋅u(t). The result reached using exponential form is correct.
Please notice that while appling the trigonometric form of Fourier transform, the factor of 1/π was ignored.
At the very end, the difference lies between "+a²" and "-ia²". I believe that I should have gotten "-ia²" instead of +a²" for A(α)+B(α) result. The error might be somewhere in the calculation for B(α), or the reason might be ignoring the factor of 1/π.
Could you please help me with tracing down that error? Thank you!


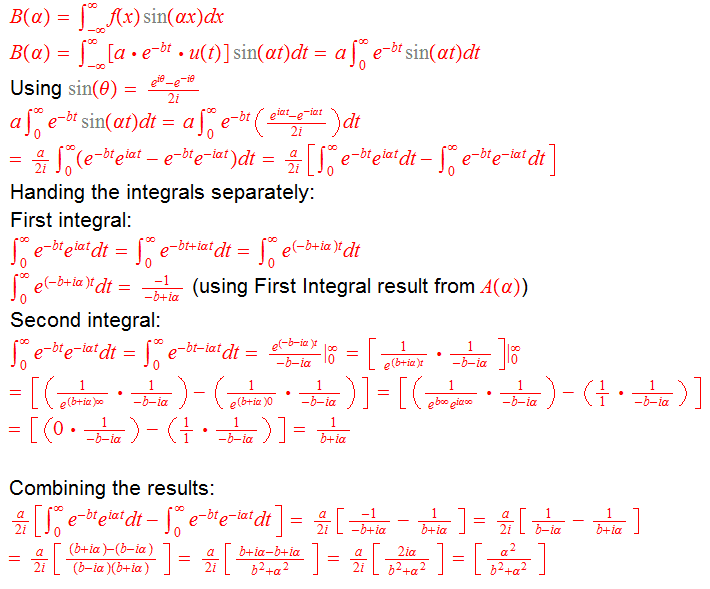
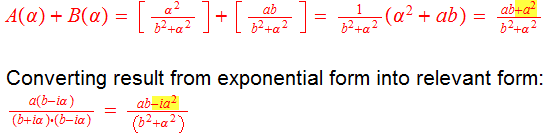
I tried to apply different forms of Fourier transform, exponential and trigonometric forms, to the same function, f(t)=a⋅e^-(bt)⋅u(t). The result reached using exponential form is correct.
Please notice that while appling the trigonometric form of Fourier transform, the factor of 1/π was ignored.
At the very end, the difference lies between "+a²" and "-ia²". I believe that I should have gotten "-ia²" instead of +a²" for A(α)+B(α) result. The error might be somewhere in the calculation for B(α), or the reason might be ignoring the factor of 1/π.
Could you please help me with tracing down that error? Thank you!
