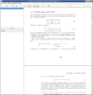
Fourier series equation derivation
- Context: Graduate
- Thread starter merlyn
- Start date
Click For Summary
Discussion Overview
The discussion revolves around the derivation of an equation related to exponential Fourier series, specifically focusing on the transformation of the left-hand side of an equation into its right-hand side. Participants seek detailed steps and clarification on integrating exponential functions within this context.
Discussion Character
- Technical explanation
- Homework-related
- Debate/contested
Main Points Raised
- One participant requests a detailed derivation of an equation from an attachment, indicating a need for assistance with exponential Fourier series.
- Another participant emphasizes that while they are willing to help, they will not complete the work for the requester, prompting them to start from the left-hand side of the equation.
- A participant mentions their background and attempts to convert the equation to Euler's form, expressing difficulty in applying trigonometric identities.
- Several participants discuss the integration of exponential functions, with one suggesting that the integral can be simplified by collapsing the product of two exponentials.
- There is a suggestion to use integral tables or online tools to find solutions to the integral involved.
- Participants share their experiences with integral tables and express nostalgia for older mathematical resources.
- One participant provides a worked-out example of the integral, demonstrating the steps involved in the derivation process.
Areas of Agreement / Disagreement
Participants generally agree on the need for a detailed derivation and the importance of understanding the integration of exponential functions. However, there are differing levels of familiarity with the material, and some participants express uncertainty about specific steps in the derivation process.
Contextual Notes
Some participants mention challenges related to integrating exponentials and the need for more than just a list of integrals to grasp the concepts of Fourier series. There is also a reference to potential confusion regarding the presentation of mathematical expressions.
Similar threads
- · Replies 33 ·
- · Replies 23 ·
- · Replies 11 ·
- · Replies 5 ·
- · Replies 8 ·
- · Replies 9 ·
- · Replies 7 ·
- · Replies 3 ·
- · Replies 2 ·
- · Replies 5 ·