Discussion Overview
The discussion revolves around the possibility of creating a Fourier series expansion for a step function, particularly focusing on increasing or decreasing step functions. Participants explore the mathematical implications and methods of handling such functions in the context of Fourier analysis.
Discussion Character
- Exploratory, Technical explanation, Debate/contested
Main Points Raised
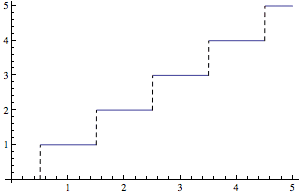
- One participant inquires about the feasibility of a Fourier series expansion for a step function, seeking to understand the underlying idea.
- Another participant states that while integrals can be written down, they will diverge for infinite step functions, but may work for finite step functions.
- A follow-up suggests breaking the function into segments where it is constant and calculating the integral for each segment before summing them.
- Concerns are raised about the divergence of the sum for most frequencies, questioning the validity of the approach for certain frequencies.
- A participant expresses a desire to extract a mathematical function from a graph of voltage response, seeking guidance on how to proceed.
- Another participant proposes representing the function as a sum of a linear or parabolic function combined with a periodic term, while expressing skepticism about the utility of this approach compared to a piecewise definition.
Areas of Agreement / Disagreement
Participants exhibit disagreement regarding the methods and feasibility of applying Fourier series to step functions, with no consensus reached on the best approach or validity of certain methods.
Contextual Notes
Limitations include the divergence of integrals for infinite step functions and the potential complications in applying Fourier series to such functions. The discussion also highlights the need for careful consideration of function definitions and the conditions under which the Fourier series may be applicable.