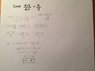Fractional equations w/ binomial denominators

[DS2C]

Homework Statement

D+8/D-2 = 9/4

See image, original equation in black.

Homework Equations

The Attempt at a Solution

See image.

Having a little trouble with this.
Ive attempted to solve it two ways. The first was to multiply both sides by $d-2$ which gave me the correct answer of $d=10$.
However when I try it the other way, by multiplying both sides by the LCD, the answer is incorrect. This method is the method I used in the attached picture.
What have I done wrong? I am assuming its because I am changing te LCD from $4\left(d-2\right)$ to $4d-8$ which technically isn't the LCD anymore, but without doing this I don't see how I can multiply the original LCD throughout the equation.

 

[DS2C]

Nevermind, I found the problem. I could have canceled the $d-2$ right off the bat with the original setup. Doing this gave me the $d=10$
But I still have the question with the LCD:
Can I take the LCD of $4\left(d-2\right)$ and change it to $4d-8$ from the start, or since this is not the LEAST common denominator it would not work?

 

[Mark44]

D+8/D-2 = 9/4

When you write fractions like these on one line, you need parentheses around the numerator and around the denominator.
What you have above means $D + \frac 8 D - 2 = \frac 9 4$, which is different from what's in your image.

Nevermind, I found the problem. I could have canceled the $d-2$ right off the bat with the original setup. Doing this gave me the $d=10$
But I still have the question with the LCD:
Can I take the LCD of $4\left(d-2\right)$ and change it to $4d-8$ from the start, or since this is not the LEAST common denominator it would not work?

Because of the d - 2 denominator, you should explicitly note (in writing) that d cannot be 2. Otherwise you are dividing by zero.

Regarding the LCD, it doesn't matter if you multiply by something that is a multiple of the LCD. The reason for the multiplication is to get rid of all fractions on both sides, so you might end up with something like 9x = 24 instead of 3x = 8, both of which simplify to x = 8/3. (This is just an example, unrelated to your problem.)

Finally, when you have obtained a solution, check your answer by substituting into the original equation. If your answer is correct you'll end up with an equation that is identically true. In your first post, you had an answer of d = 2. This can't be the solution because it makes the denominator on the left side zero, and you can't divide by zero.

 

[DS2C]

Ok that makes sense with that portion.
Still a little confused in regards to find the LCD for binomials.
If I have $y-2$, $2$, and $2y-4$, is my LCD going to be $2y-4$? Do the signs matter at all? Or is the absolute value the only thing that matters in regards to the LCD here?

 

[Mark44]

Ok that makes sense with that portion.
Still a little confused in regards to find the LCD for binomials.
If I have $y-2$, $2$, and $2y-4$, is my LCD going to be $2y-4$? Do the signs matter at all? Or is the absolute value the only thing that matters in regards to the LCD here?

2y - 4 = 2(y - 2), so the least common multiple (LCM) of 2 and y - 2 is 2(y - 2). The signs don't enter into things here, so I don't know why you're asking about them.

Regarding your question in post #2:

But I still have the question with the LCD:
Can I take the LCD of $4(d-2)$ and change it to $4d-8$ from the start

Forget LCD, or more accurately, LCM for the moment. 4(d - 2) is identically equal to 4d - 8, so you can always change either one to the other.

, or since this is not the LEAST common denominator it would not work?

If the problem were $\frac{6}{2(d - 2)} = \frac 9 4$, you could multiply both sides by $4 \cdot 2(d - 2)$, and that would clear the fractions on both sides. This is true even though 4(2)(d - 2 ) isn't the least common multiple of 4 and 2(d - 2). The LCM is actually 4(d - 2), which is the simplest expression that is evenly divisible by 4 and 2(d - 2). It's just most efficient if you clear fractions by multiplying by the LCM rather than by some larger multiple of it.