Free Body Diagram Explained: Why is Right FBD Upward?

Click For Summary
SUMMARY

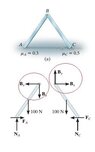
The discussion centers on the interpretation of Free Body Diagrams (FBD) in the context of Newton's Third Law of Motion. Participants clarify that for every action, there is an equal and opposite reaction, which explains the upward force component in the FBD. The conversation also addresses the discrepancy between the number of unknown forces in the FBD, with the conclusion that the coefficients of friction provide an additional equation, thereby reducing the number of unknowns to three: the horizontal components (bx), the vertical component (by), and the normal force (Na).

PREREQUISITES
  • Understanding of Newton's Third Law of Motion
  • Familiarity with Free Body Diagrams (FBD)
  • Basic knowledge of friction coefficients
  • Ability to analyze forces in two dimensions
NEXT STEPS
  • Study the application of Newton's Laws in static equilibrium problems
  • Learn about the role of friction in mechanical systems
  • Explore advanced Free Body Diagram techniques for complex structures
  • Investigate the implications of multiple unknown forces in engineering analysis
USEFUL FOR

Students of physics, engineering students, and professionals involved in mechanics and structural analysis will benefit from this discussion.

Drain Brain
Messages
143
Reaction score
0
Can you explain why the free body diagram of each members are as shown? I kind of understand why the FBD of the member on the left is drawn as shown. But the FBD on the right is confusing, Why does it have a component in Y (upward) direction?
thanks!
 

Attachments

  • statics friction.jpg
    statics friction.jpg
    12 KB · Views: 129
Mathematics news on Phys.org
Drain Brain said:
Can you explain why the free body diagram of each members are as shown? I kind of understand why the FBD of the member on the left is drawn as shown. But the FBD on the right is confusing, Why does it have a component in Y (upward) direction?
thanks!

Hi Drain Brain!

It's Newton's 3rd law: whenever a body pushes against another body, that body pushes back with an equal and opposite force.
For the horizontal forces that should be intuitive.
For the vertical forces we pick one down, meaning the other must be up.
 
I like Serena said:
Hi Drain Brain!

It's Newton's 3rd law: whenever a body pushes against another body, that body pushes back with an equal and opposite force.
For the horizontal forces that should be intuitive.
For the vertical forces we pick one down, meaning the other must be up.

Hi I Like Serena! Now I understand!

There's another thing I want to ask, my book says that there are 3 unknown forces on each member, but I see 4 unknowns. Can you tell me why that is?
 
Drain Brain said:
Hi I Like Serena! Now I understand!

Good!

There's another thing I want to ask, my book says that there are 3 unknown forces on each member, but I see 4 unknowns. Can you tell me why that is?

They're probably jumping a bit ahead.
Since the coefficients of friction are given, that gives us the extra equation $F_A=\mu_A N_A$, effectively eliminating $F_A$ as an unknown.
 
I like Serena said:
Good!
They're probably jumping a bit ahead.
Since the coefficients of friction are given, that gives us the extra equation $F_A=\mu_A N_A$, effectively eliminating $F_A$ as an unknown.

Do you mean to say that the 3 unknown forces my book is referring to are the components bx, by and the normal force Na?
 
Drain Brain said:
Do you mean to say that the 3 unknown forces my book is referring to are the components bx, by and the normal force Na?

That's what I expect yes.
 

Similar threads

Why are moments not included in free body diagrams?
  • · Replies 31 ·
2
Replies
31
Views
2K
High School Elevator Question -- What does a downward acceleration mean?
  • · Replies 4 ·
Replies
4
Views
2K
Is it friction or tension acting on the person hanging on a rope?
  • · Replies 4 ·
Replies
4
Views
1K
Need Help with Free Body Diagram of Oil & Gas Packer Tool
  • · Replies 2 ·
Replies
2
Views
1K
Center of mass and momentum- A question about systems
  • · Replies 25 ·
Replies
25
Views
2K
MHB Free Body Diagram Solve Problem: Find Force Normal
  • · Replies 5 ·
Replies
5
Views
3K
Undergrad Systems and number of FBDs....
  • · Replies 8 ·
Replies
8
Views
2K
Beam boundary condition problem
  • · Replies 12 ·
Replies
12
Views
3K
Proper free-body diagram for a shaft experiencing multiple torques
  • · Replies 13 ·
Replies
13
Views
5K
Engineering Should one include friction in this free-body diagram?
  • · Replies 3 ·
Replies
3
Views
2K