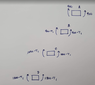Proper free-body diagram for a shaft experiencing multiple torques

[Qube]

Homework Statement

Draw a FBD, determine the largest torque, T1, and find shear stresses in CD and DE

Relevant Equations

Method of sections, static equilibrium
shear stress=Tc/J

I wish to draw a proper free-body diagram for this shaft. However, my FBD does not agree with the solutions manual. If someone could point out where I erred, that would be great.

This is what I drew:

From my FBD, it is clear that the maximum torque is present in section DE of the shaft.

We can use the equation shear stress=Tc/J in conjunction with the maximum allowed shear stress of 60 MPa as follows:

Then, to find the maximum shear stresses in sections CD and DE:

 

[haruspex]

Are you sure about the $\frac{\pi}4$s? I thought it was $\frac{\pi}2$

 

[Qube]

Thanks! You are right, it is J=pi*c^4/2. I will rework this problem and see if I get the right answer this time...

 

[haruspex]

Thanks! You are right, it is J=pi*c^4/2. I will rework this problem and see if I get the right answer this time...

Note that with your original calculation the 900Nm was already too much for AB.

 

[Qube]

Okay, I reworked the problem. I drew a torque diagram.

It seems that the maximum possible value of the unknown torque, T1, is 327 Nm.

From there, it seems that the internal shear stress in section CD is about 47 MPa, and the internal torque in DE causes the bar to hit its shear stress limit, 60 MPa.

This makes much more sense than my initial results.

Does it make sense that the section with the highest shear stress is the section of the bar closest to the wall, to which the bar is anchored?

Also, does my torque diagram make sense? Someone else argues that this is the correct diagram:

 

[haruspex]

Okay, I reworked the problem. I drew a torque diagram.

View attachment 270516

It seems that the maximum possible value of the unknown torque, T1, is 327 Nm.

From there, it seems that the internal shear stress in section CD is about 47 MPa, and the internal torque in DE causes the bar to hit its shear stress limit, 60 MPa.

View attachment 270517

This makes much more sense than my initial results.

Does it make sense that the section with the highest shear stress is the section of the bar closest to the wall, to which the bar is anchored?

Also, does my torque diagram make sense? Someone else argues that this is the correct diagram:

View attachment 270518

What, exactly, is the inequality involving 1800 - T₁ that you deduce from your diagram?
What will happen to your diagram if T₁ is increased a little?
What would happen if T₁ were zero?

 

[Qube]

Okay, scratch all that. I managed to figure it out by finding similar problems. Thank you for the guidance. I hope that this post of mine is error-free!

We need to start by applying the right-hand rule to the applied torques, with the sign convention that a torque directed away from point E is a positive torque. This means A, C, and D are positive, and the unknown torque at B (T1) is a negative torque.

With the above established, we can find the internal torque in segment AB, knowing that the segment is in equilibrium:

We also know that the maximum allowable shear stress in any segment is 60 MPa, which allows us to find the maximum value of T1:

Using the above information, and the fact that every section of the bar is in equilibrium, we can find the internal torques of each section.

Knowing the internal torques of sections CD and DE allow us to find the maximum shear stresses within CD and DE.

 

[haruspex]

That's unnecessarily rewriting what you did successfully in post #5 by other means.
You found that the torques are, taking some sign convention, 900, 900-T, 1500-T, 1800-T.
The constraint is some maximum magnitude torque, T_max. What is the correct way to write that algebraically?

 

[Qube]

You found that the torques are, taking some sign convention, 900, 900-T, 1500-T, 1800-T.
The constraint is some maximum magnitude torque, T_max. What is the correct way to write that algebraically?

I don't understand, but I'll give it a try.

Are you saying to plug 900-T, 1500-T, and 1800-T into the equation, shear=Tc/J and try to maximize the value of T?

 

[haruspex]

I don't understand, but I'll give it a try.

Are you saying to plug 900-T, 1500-T, and 1800-T into the equation, shear=Tc/J and try to maximize the value of T?

No, I am asking how you express in algebra that, e.g., the torque 1500-T must not exceed the calculated limit (call it T_max)? Be careful.

 

[Qube]

1500-T<Tmax

I'm still unclear on what you mean, sorry.

 

[haruspex]

1500-T<Tmax

View attachment 270636

I'm still unclear on what you mean, sorry.

It's magnitudes!

 

[Qube]

It's magnitudes!

I don't see a direct constraint on Tmax in this problem that is given. I'm still unclear on what you mean by:

The constraint is some maximum magnitude torque, Tmax. What is the correct way to write that algebraically?

The only constraint I see is on torsional shear, which is a function of Tmax.

 

[haruspex]

I don't see a direct constraint on Tmax in this problem that is given. I'm still unclear on what you mean by:
The only constraint I see is on torsional shear, which is a function of Tmax.

I was using Tmax to mean the maximum torsional shear, not the max value of T1.
I'll stop trying to be subtle. You computed 900-T1, 1500-T1, and 1800-T1, and took the constraint to be that each < Tmax. In fact, the constraint is on the magnitudes of these: |900-T1|<Tmax, |1500-T1|<Tmax, and |1800-T1|<Tmax. That opens up more possibilities.