Free fall question, where has my reasoning gone wrong?

[emyt]

Hi, I'm having some trouble finishing the second part... here's the question again for quick reference

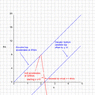
An elevator ascends with an upward acceleration of 4.0ft/s^2. At the instant its upward speed is 8.0ft/s, a loose bolt drops from the ceiling of the elevator 9.0 ft from the floor.

Calculate (a) the time of flight of the bolt from the ceiling to the floor

(b) the distance it has fallen relative to the elevator shaft.

Answer: (a) 0.71 (b) 2.3 ft

I supposed that at some point in time, the velocity is at 10.84, since vx = vx0 + axt --> vx = 8.0 + 4.0(0.71)--> 8.0 + 2.84 = 10.84

now since we're talking about the elevator shaft, I set x0 to zero and attempted to solve for x with various equations.. I can't seem to do it.. Could someone please give me some advice?

thanks

also, in one dimensional motion, if x = 0 vx0 would equal to 0 as well right? so we can say that Vx0 = 0?

 

[Doc Al]

I supposed that at some point in time, the velocity is at 10.84, since vx = vx0 + axt --> vx = 8.0 + 4.0(0.71)--> 8.0 + 2.84 = 10.84

That's the velocity of the elevator at the moment the bolt hits the floor. You won't need that.

now since we're talking about the elevator shaft, I set x0 to zero and attempted to solve for x with various equations.. I can't seem to do it.. Could someone please give me some advice?

You use the same equations you used to solve part a. I would set the initial position of the bolt to be x0 = 9 and the initial position of the elevator floor to be x0 = 0.

also, in one dimensional motion, if x = 0 vx0 would equal to 0 as well right? so we can say that Vx0 = 0?

No, that's not true. You should know what Vx0 is by now!

 

[DaveC426913]

I don't understand. Why do you keep thinking that the initial velocity is zero?

 

[emyt]

I don't understand. Why do you keep thinking that the initial velocity is zero?

I don't, after failing to find out how to solve the 2nd part I was wondering if x = 0 in one dimensional motion implied that the velocity is 0... since x/ time?

thanks

 

[emyt]

That's the velocity of the elevator at the moment the bolt hits the floor. You won't need that.


You use the same equations you used to solve part a. I would set the initial position of the bolt to be x0 = 9 and the initial position of the elevator floor to be x0 = 0.



No, that's not true. You should know what Vx0 is by now!

thanks, damn. I thought I was on the right track - vx0 being 0 or not, I thought that if I could find the position of the bolt in the elevator shaft by setting x0 = 0 and finding the time it would take to get to the velocity of the elevator at that point..et c

 

[bleedblue1234]

this is the full question:

An elevator ascends with an upward acceleration of 4.0ft/s^2. At the instant its upward speed is 8.0ft/s, a loose bolt drops from the ceiling of the elevator 9.0 ft from the floor.

Calculate (a) the time of flight of the bolt from the ceiling to the floor

(b) the distance it has fallen relative to the elevator shaft.

Answer: (a) 0.71 (b) 2.3 ft

Here I will solve (good practice for AP physics anyways)

So first let's do the time from dropping to the time where it returns to the original drop height...

first conversions:
8.0ft = 2.4384 meters
9.0ft= 2.7432 meters

so just do this

-2.7432 = -2.4384t + 1/2(-9.80)t^2

so

0 = (-4.9)t^2 + (-2.4384)t + 2.7432

so use quadratic formula

t = (2.4384 + sqrt(-2.4384^2 * 4(-4.9)(2.7432))) / (2*-4.9)

so i had t=.540 s

 

[emyt]

this is the full question:

An elevator ascends with an upward acceleration of 4.0ft/s^2. At the instant its upward speed is 8.0ft/s, a loose bolt drops from the ceiling of the elevator 9.0 ft from the floor.

Calculate (a) the time of flight of the bolt from the ceiling to the floor

(b) the distance it has fallen relative to the elevator shaft.

Answer: (a) 0.71 (b) 2.3 ft

Here I will solve (good practice for AP physics anyways)

So first let's do the time from dropping to the time where it returns to the original drop height...

first conversions:
8.0ft = 2.4384 meters
9.0ft= 2.7432 meters

so Vy = Vyo + gt

so -2.4384 = 2.4384 + (-9.80)t

so -4.8768 = (-9.80)t

so t = .4976326531 (i will store this in my calculator)

So now we know the time from dropping to the time where it is once against at the drop height...

so now we need to find the time from the original height to the floor...

(delta) y = Vyot + 1/2gt^2

2.7432 m = -4.8768t + 1/2(-9.8)t^2

so 0 = -4.9t^2 + -4.8768t + -2.7432 m

so use quadratic equation

t = (4.8768 - sqrt(-4.8768^2 - 4(-4.9)(-2.7432)))/2(-4.9)

so t=9.627132911 (store in calculator)

so if you add both t's you get 10.1 seconds

the question doesn't ask you for the time for the elevator shaft?

 

[bleedblue1234]

the question doesn't ask you for the time for the elevator shaft?

?

i must have done my math wrong but i am sure the way to solve it is correct..

 

[emyt]

?

i must have done my math wrong but i am sure the way to solve it is correct..

what is 10.1 seconds supposed to be?

 

[bleedblue1234]

i calculated the time from the bolt dropping to the time it hit the ground, but i think the correct answer is around .5 ish seconds...

 

[emyt]

i calculated the time from the bolt dropping to the time it hit the ground, but i think the correct answer is around .5 ish seconds...

you mean dropping to the floor of the elevator? that should be 0.71 seconds

 

[bleedblue1234]

you mean dropping to the floor of the elevator? that should be 0.71 seconds

oooo i thought you were dropping from the top of the elevator to the bottom of the shaft... that's different

 

[emyt]

oooo i thought you were dropping from the top of the elevator to the bottom of the shaft... that's different

no, that's not the question.. how would you do what is actually stated there?

thanks

 

[DaveC426913]

Have you tried to draw a graph of the problem? I think a graph showing v/t might help you visualize the components better.

 

[emyt]

Have you tried to draw a graph of the problem? I think a graph showing v/t might help you visualize the components better.

I haven't tried drawing a graph but I've already drawn graphs to visualize the components of a velocity vector. but this problem has motion in 1 dimension right? so it's just a graph of x versus time?

thanks

 

[DaveC426913]

I haven't tried drawing a graph but I've already drawn graphs to visualize the components of a velocity vector. but this problem has motion in 1 dimension right? so it's just a graph of x versus time?

thanks

Yes.

 

[DaveC426913]

What am I doing wrong in this graph?

I'm having trouble figuring how to skew the bolt drop slope to account for the initial velocity.

I've skewed it by y=1 across x=1. (faint pink line almost visible to left of red line)


Clearly I've got it very wrong since it shows a fall lasting only .25s.

 

[Doc Al]

thanks, damn. I thought I was on the right track - vx0 being 0 or not, I thought that if I could find the position of the bolt in the elevator shaft by setting x0 = 0 and finding the time it would take to get to the velocity of the elevator at that point..et c

Start by showing how you solved part a. What you should have done to solve it, is equate expressions for the position of the bolt and the floor of the elevator (with respect to the shaft or ground) as a function of time. You solve for the time when both are at the same place. Then just plug that time into get the position.

 

[Doc Al]

Here I will solve (good practice for AP physics anyways)

So first let's do the time from dropping to the time where it returns to the original drop height...

first conversions:
8.0ft = 2.4384 meters
9.0ft= 2.7432 meters

so just do this

-2.7432 = -2.4384t + 1/2(-9.80)t^2

so

0 = (-4.9)t^2 + (-2.4384)t + 2.7432

so use quadratic formula

t = (2.4384 + sqrt(-2.4384^2 * 4(-4.9)(2.7432))) / (2*-4.9)

so i had t=.540 s

Please do not (attempt to) provide complete solutions. Let the OP figure it out!

 

[Doc Al]

What am I doing wrong in this graph?

You show a speed vs time graph, yet the top and bottom of the elevator car are on different lines. (I think we can safely assume that they have the same speed!)

Draw a position vs time graph.

 

[DaveC426913]

You show a speed vs time graph, yet the top and bottom of the elevator car are on different lines. (I think we can safely assume that they have the same speed!)

Draw a position vs time graph.

Right.

Going back & forth between d/t and v/t graphs messed me up.

I couldn't do the d/t because PhotoShop doesn't plot a parabola very well.

 

[emyt]

hi, I solved it.. I just didn't know what they meant by "distance fallen relative to the elevator shaft". I was trying to find the position of the fallen bolt relative to the elevator shaft, but distance fallen is a different thing.

but distance fallen in units isn't relative to anything is it? if something falls x amount of km, it has fallen x amount of km's no matter how you look at it? thanks

 

[Doc Al]

hi, I solved it.. I just didn't know what they meant by "distance fallen relative to the elevator shaft". I was trying to find the position of the fallen bolt relative to the elevator shaft, but distance fallen is a different thing.

Finding the change in position of the bolt with respect to the elevator shaft will tell you the distance fallen with respect to the shaft.

but distance fallen in units isn't relative to anything is it? if something falls x amount of km, it has fallen x amount of km's no matter how you look at it?

No, the distance fallen very much depends on what you're measuring with respect to. For example, how far the bolt falls with respect to the elevator car is quite different than how far it falls with respect to the shaft.

 

[willem2]

but distance fallen in units isn't relative to anything is it? if something falls x amount of km, it has fallen x amount of km's no matter how you look at it?


thanks

I would say it does matter.

someone in the elevator will think it has fallen 9 feet. that's why they said "relative to
the elevator shaft"

 

[emyt]

No, the distance fallen very much depends on what you're measuring with respect to. For example, how far the bolt falls with respect to the elevator car is quite different than how far it falls with respect to the shaft.

Could you give me an example? if you say something like "the bolt fell 2 feet into the elevator" then how much will it have fallen from the perspective of the shaft? it would still be a fall of 2 feet wouldn't it?

Finding the change in position of the bolt with respect to the elevator shaft will tell you the distance fallen with respect to the shaft.

I'm not sure what it means entirely to say "change in position with respect to the elevator shaft" :S Does it mean to find the position of the bolt in the elevator shaft (so instead of 9 feet it would be like 25 feet or something), and then find the position of the bolt after 0.71 seconds and see the difference? This is what I thought before, but if it falls in 0.71 x amount of feet, then why would it make a difference if you were considering the bolt 9 feet in the air or 25 feet in the air?

Start by showing how you solved part a. What you should have done to solve it, is equate expressions for the position of the bolt and the floor of the elevator (with respect to the shaft or ground) as a function of time. You solve for the time when both are at the same place. Then just plug that time into get the position.

yes I did that, but plugging in the time to get the position is the position in respect to the elevator right? Well, I did that and I took the difference between the elevators initial position and the new position, giving me the answer.. but now I'm confused because of what you guys are now saying

thanks

 

[Doc Al]

Could you give me an example? if you say something like "the bolt fell 2 feet into the elevator" then how much will it have fallen from the perspective of the shaft? it would still be a fall of 2 feet wouldn't it?

No. Here's a reverse example. Say you are in an elevator car and you drop a ball at the instant the cable breaks (and thus you are in free fall--forget about brakes or friction). Say you start out on the 100th floor and after some time you crash into the bottom of the shaft. During that fall, how far did the ball move with respect to the elevator car? Obviously you've fallen 100 floors with respect to the shaft.

I'm not sure what it means entirely to say "change in position with respect to the elevator shaft" :S Does it mean to find the position of the bolt in the elevator shaft (so instead of 9 feet it would be like 25 feet or something), and then find the position of the bolt after 0.71 seconds and see the difference?

Exactly.

This is what I thought before, but if it falls in 0.71 x amount of feet, then why would it make a difference if you were considering the bolt 9 feet in the air or 25 feet in the air?

It doesn't. All that matters is the change in position.

 

[emyt]

No. Here's a reverse example. Say you are in an elevator car and you drop a ball at the instant the cable breaks (and thus you are in free fall--forget about brakes or friction). Say you start out on the 100th floor and after some time you crash into the bottom of the shaft. During that fall, how far did the ball move with respect to the elevator car? Obviously you've fallen 100 floors with respect to the shaft.

oh okay, right. if you said something like x amount of feet from the elevator car or x amount of feet down the shaft, then it would be different.. then if you just measured the feet fallen without respect to anything what would you call that

Exactly.

It doesn't. All that matters is the change in position.

Okay, I'm not sure if I did it correctly, I found the amount of feet it fell from its initial position to its new position. I'm not sure how it's relative to the elevator shaft though.

thanks

 

[Doc Al]

then if you just measured the feet fallen without respect to anything what would you call that

A meaningless number.

Okay, I'm not sure if I did it correctly, I found the amount of feet it fell from its initial position to its new position. I'm not sure how it's relative to the elevator shaft though.

If you had an expression for the position of the bolt, it must have been with respect to something (even if you aren't quite sure to what). Show the expression that you used. (I'm sure it was with respect to the shaft/ground.)

 

[emyt]

A meaningless number.

If you had an expression for the position of the bolt, it must have been with respect to something (even if you aren't quite sure to what). Show the expression that you used. (I'm sure it was with respect to the shaft/ground.)

first, for part a, I solved for the time by

9 + 8t -16t^2 = 8t + 2t^2

and then I got sqrt(9/18) which is 0.71 seconds.

then I plugged 0.71 into 9+8t - 16t^2 to see the new position it fell to.. then I took that position (6.680 feet) and subtracted it from the original 9 feet to get the distance fallen. I got 2.3 ft, but that led me the question about whether it mattered where I took the distance from and if it even mattered that I took the distance fallen from 9 feet in the air or 25 feet in the air - since I couldn't find the position of the bolt in the elevator shaft. but say, if I found out that the bolt was 15 feet in the air from the elevator shaft, the distance fallen from 9 to 6.680 would be the same as the distance fallen from 15 feet to 12.7 feet. thanks

 

[Doc Al]

first, for part a, I solved for the time by

9 + 8t -16t^2 = 8t + 2t^2

Good. Note that each side is the position with respect to the shaft. You don't know the actual height of the bolt or elevator floor, but all that matters is that the bolt starts off 9 ft higher than the elevator floor. Your equation just assumes that the elevator floor is at position y0 = 0, which is fine. (Who cares?)

Note that if you assumed that the elevator floor was initially at y0 = 25 ft and thus the bolt was at y0 = 25+9 = 34 ft, that nothing would change. The arbitrary 25ft would just drop out of the equation when you solved for the time or the change in position.

But all of your position measurements are with respect to the shaft.