Discussion Overview
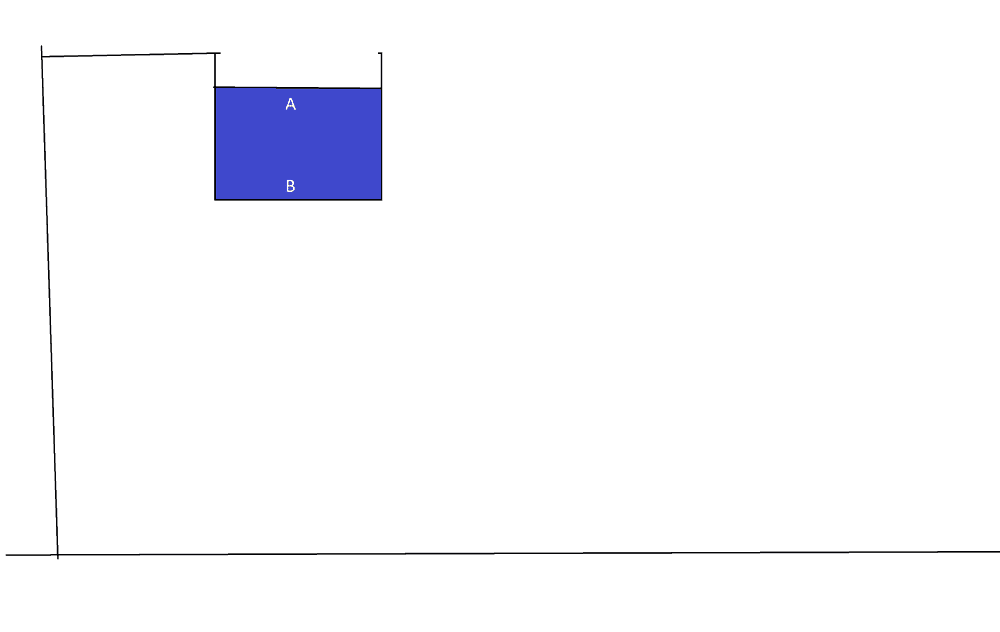
The discussion revolves around the hydrostatic pressure in a water tank that is in freefall, specifically comparing the pressure at two points: A at 0.1m depth and B at 10m depth. Participants explore the effects of acceleration and constant velocity on hydrostatic pressure, addressing both theoretical and conceptual aspects of fluid dynamics in a freefall scenario.
Discussion Character
- Exploratory
- Technical explanation
- Conceptual clarification
- Debate/contested
Main Points Raised
- Some participants question whether hydrostatic pressure at point A is greater than at point B during the acceleration phase (0-5 seconds).
- Others assert that after 5 seconds, when the tank is moving at constant speed, the hydrostatic pressure at both points should be the same.
- One participant suggests that during freefall, the water does not exert pressure on the layers below it due to the lack of vertical forces, creating no pressure difference until steady speed is reached.
- Another participant raises the issue of normal force and air drag during freefall, questioning how these forces interact with the water's behavior.
- Some participants discuss the sensation of weightlessness during freefall and how it relates to the behavior of internal organs and pressure sensations.
- There is a suggestion that during the accelerating phase, air resistance affects the tank's acceleration, potentially leading to a slight increase in pressure at point B compared to point A.
- A later reply discusses the extreme pressure conditions when the water hits the ground at terminal velocity, including the dynamics of splashing and energy transfer upon impact.
Areas of Agreement / Disagreement
Participants express differing views on the relationship between hydrostatic pressure at points A and B during the acceleration phase and after reaching constant speed. There is no consensus on the effects of air resistance and the implications for pressure differences. The discussion remains unresolved regarding the exact nature of pressure changes throughout the freefall process.
Contextual Notes
Participants mention various assumptions, such as the effects of air resistance and the definition of freefall, which may influence their arguments. The discussion includes references to the transition between freefall and terminal velocity, highlighting the complexity of the fluid dynamics involved.