- #1
RiotRick
- 42
- 0
Homework Statement
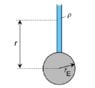
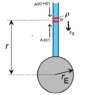
There is an infnite high hydrostatic head in an infite high tank on the surface of earth. How big is the pressure p(r) in tank at a distance r. Ignore the rotation of the Earth and assume the water stays liquid. ( So basically ignore it's an impossible scenario )
Instruction: Look at a mass element with thickness dr and establish the condition of equilibrium between gravitational force and pressure force. You'll get a differential equation. Then use the fact that ##p(r \rightarrow \infty )## is 0.
Try to give an answer without G and M. G is the gravitational constant and M the mass of the earth
Homework Equations
Given:
##g,r,r_E,\rho,M## M is the mass of the earth
##G*\frac{M*m}{r^2}=F_g##
The Attempt at a Solution
[/B]
I'don't fully understand how set up the equillibrium condition.
So the Earth is pulling the water:
##G*\frac{M*m}{(r)^2}=m*g##
but the water dr away pulls the water in the opposite direction but is also pulled towards the earth. I don't see it.