piacere_space
- 2
- 0
The car weighs 15kN. The coefficient of static friction between the car tires and the road is \mus=0.5. Determine the steepest grade (the largest value of the angle of \alpha) the car can drive up at constant speed if the car has (a) rear-wheel drive, (b) front-wheel drive, and (c) four-wheel drive.
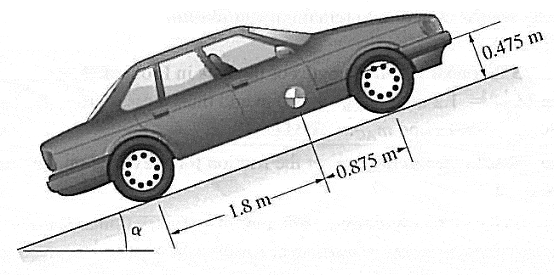
My answers are (a)10.18o (b)17.17o (c)26.57o. I just wonder if they are really correct. Thanks!
Sorry yeah I forgot to post my attempt...
Let the normal forces at the rear wheel and the front wheel be NA and NB respectively. Also let the contact points at the rear and front wheel be A and B respectively.
(a)(1)0.5NA-15sin\alpha=0 then NA=30sin\alpha (2)0.875*15cos\alpha+0.475*15sin\alpha-2.675NA=0 then 13.125cos\alpha+7.125sin\alpha-2.675NA=0. Now from (1) and (2) tan\alpha=7/39 then \alpha=10.18o
Here I assume the rolling friction at the point B is ignorable. (1) is about the equilibrium of all forces in the horizontal direction. (2) is about the equations of moments around B.
Basically I did the same things for (b) and (c).
(b)tan\alpha=72/233 then \alpha=17.17o
(c)tan\alpha=0.5 then \alpha=26.57o
My answers are (a)10.18o (b)17.17o (c)26.57o. I just wonder if they are really correct. Thanks!
Sorry yeah I forgot to post my attempt...
Let the normal forces at the rear wheel and the front wheel be NA and NB respectively. Also let the contact points at the rear and front wheel be A and B respectively.
(a)(1)0.5NA-15sin\alpha=0 then NA=30sin\alpha (2)0.875*15cos\alpha+0.475*15sin\alpha-2.675NA=0 then 13.125cos\alpha+7.125sin\alpha-2.675NA=0. Now from (1) and (2) tan\alpha=7/39 then \alpha=10.18o
Here I assume the rolling friction at the point B is ignorable. (1) is about the equilibrium of all forces in the horizontal direction. (2) is about the equations of moments around B.
Basically I did the same things for (b) and (c).
(b)tan\alpha=72/233 then \alpha=17.17o
(c)tan\alpha=0.5 then \alpha=26.57o
Attachments
Last edited: