- #1
wallism
- 8
- 0
Hi, this problem’s been bugging me for ages. I’m sure it’s just a simple misunderstanding somewhere on my behalf but I just can’t seem to get my head round it.
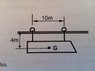
A monorail car with front wheel drive and mass of 5 tonnes is suspended from two wheels 10m apart as shown. Its centre of mass G is midway between the wheels and 4m below the rail.
Starting from rest, the train is designed to achieve a maximum speed of 20km/h in 40s with uniform acceleration. Calculate the minimum coefficient of friction between the front wheel and the rail to achieve this.
Part 2
Determine the acceleration that could be achieved with the same coefficient of friction if rear wheel drive was used, and hence the time to reach 200km/hr.
The answers given are 0.254 and 49.1
I've attached a photo of the diagram.
F=ma
F=uR
V=at
1. Firstly calculate the acceleration in m/s^2
To do this I converted the speed
200 km/hr is equivalent to 200x10^3 m/hr
Divide into seconds 200x10^3/3600 = 55.5 m/s
Then divide by 40s to get the acceleration needed (v/t=a)so a = 1.38ms^-2 or 25/18
2. Calculate the force needed to accelerate the mass
F=ma, m=5000kg, a=1.38ms^-2
5000 x 1.38 = 6944.4N or 62500/9
3. Work out the coefficient of friction.
a) Work out the reaction force of the front wheel on the beam, using moments and resolving forces, giving you 24525N (2500kg x 9.81)
b) Use F=uR
Calculated F needed as 6944.4, and R as 24525N
Rearrange formula F/R=u
6944.4/24525 = 0.283 which is wrong!?
Surely the centre of mass G must affect it somehow but I don’t understand how to incorporate that. I can’t do the second part of the question because of the reason above. If the centre of mass was off centre then I could understand how the coefficient of friction and acceleration between front and back would differ.
Any help would be greatly appreciated.
Homework Statement
A monorail car with front wheel drive and mass of 5 tonnes is suspended from two wheels 10m apart as shown. Its centre of mass G is midway between the wheels and 4m below the rail.
Starting from rest, the train is designed to achieve a maximum speed of 20km/h in 40s with uniform acceleration. Calculate the minimum coefficient of friction between the front wheel and the rail to achieve this.
Part 2
Determine the acceleration that could be achieved with the same coefficient of friction if rear wheel drive was used, and hence the time to reach 200km/hr.
The answers given are 0.254 and 49.1
I've attached a photo of the diagram.
Homework Equations
F=ma
F=uR
V=at
The Attempt at a Solution
1. Firstly calculate the acceleration in m/s^2
To do this I converted the speed
200 km/hr is equivalent to 200x10^3 m/hr
Divide into seconds 200x10^3/3600 = 55.5 m/s
Then divide by 40s to get the acceleration needed (v/t=a)so a = 1.38ms^-2 or 25/18
2. Calculate the force needed to accelerate the mass
F=ma, m=5000kg, a=1.38ms^-2
5000 x 1.38 = 6944.4N or 62500/9
3. Work out the coefficient of friction.
a) Work out the reaction force of the front wheel on the beam, using moments and resolving forces, giving you 24525N (2500kg x 9.81)
b) Use F=uR
Calculated F needed as 6944.4, and R as 24525N
Rearrange formula F/R=u
6944.4/24525 = 0.283 which is wrong!?
Surely the centre of mass G must affect it somehow but I don’t understand how to incorporate that. I can’t do the second part of the question because of the reason above. If the centre of mass was off centre then I could understand how the coefficient of friction and acceleration between front and back would differ.
Any help would be greatly appreciated.
Attachments
Last edited: