Frictional Forces: Stacked boxes, pulley with weight.

[Cal Ripken]

Homework Statement

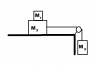
The system shown is released from rest. Mass one (0.450 kg) rests on mass two (0.820 kg) and the coefficient of static friction between the two masses is 0.560 and the same for the mass and the table. Determine the maximum mass for M(3) such that mass one will not slide on mass two. The string can be considered massless and the pulley is frictionless.

[/B]

Homework Equations

F= ma, f(static)= u(static) x n, w=mg, f(kinetic)= u(kinetic) x n.

The Attempt at a Solution

This is my free body diagram for M1, M2, and M3, respectively.
For the first FBD, according to Newton's third law, (F a on b = -F b on a), the surface of M1 exerts static friction on M2, and M2 exerts static friction on M1.
For the second FBD, I recognized that the weight would be M1+M2 times g. Also, the box would be moving and so the frictional force would be kinetic.
For the third FBD, there is only tension and weight acting on the y axis, and has no x components. Further, due to the effect of the system, I will call the downward acceleration positive.

So for the first, I know that the condition for acceleration requires that a net force act on a body. However, we want M1 to remain at rest and so
F(x) = -f(s)+f(s) = 0, F(y) = -W1 + n1 = 0

then for the second fbd
F(x) = (M1+M2)a = -f(kinetic) + T, F(y) = -W2 + n2 = 0

And for third[/B]
F(x) = 0, F(y)= -T + M3(g) = (M3)a

and so then

(M1 + M2) a = -f(kinetic) + T
+ (M3) a = (M3)g - T

= a ( (M1+M2) + (M3)) = (M3)g - f(Kinetic).

The given values are M1, M2, and a coefficient of Static friction.
according to my FBD's, Static friction cancels out. So i don't know what i did wrong there.

But, because it's a given value, and I suppose that ultimately I am looking for values of acceleration which will cause static friction to be maintained between M1 and M2, while making M3 a Maximum value:

I set f(static) = ma
u(static) X n = ma
acceleration = (u(static) X (n)) / m

so a = (0.56)(W1(g)) / (M1))

a = (0.56(4.41N)) / (0.45kg)) = 5.488 m/s^2

so this would be the maximum value for acceleration required to maintain static friction.

and so my only remaining unknown values are M3 and f(Kinetic).

I know that f(k) = u(kinetic) X n

so then f(k) is just the negative of the value for tension?

Sorry i am lost and I don't know if any of what I have done so far is correct. I suppose I would like to know if my FBD's are accurate, If my conceptual understanding is accurate, what mistakes have I made so far, am I overlooking anything? Did I approach this properly? Should I have evaluated the entire system at rest and then again in motion? Are my force components correct / did I combine the accurately? Super lost.

Thanks in advance I am an idiot =( I know this should be simple

 

[Chestermiller]

You've made a couple of mistakes with regard to Mass 1, but you are on the right track. So don't beat yourself up too much.

Mass 1 actually is accelerating since it is not yet quite slipping relative to Mass 1. A horizontal force is acting on Mass 1 at its base. This is the frictional force exerted by Mass 2 on Mass 1, and it is in the direction of movement. You correctly determined the normal force on Mass 1.

For the combination of Mass 1 and Mass 2, your horizontal force balance equation is correct, but, for the vertical direction, it is incorrect.

For Mass 3, everything is correct.

It doesn't seem possible to solve this problem unless one knows the coefficient of kinetic friction at the base of Mass 2.

Chet