Discussion Overview
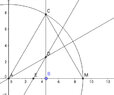
The discussion revolves around the geometric construction of points D and E in relation to a triangle, specifically to form a trapezium ACDE using only a straight edge and a compass. Participants explore the properties of triangle ACD and the relationships between angles and sides, as well as the methods for constructing the required points.
Discussion Character
- Exploratory
- Technical explanation
- Mathematical reasoning
Main Points Raised
- Some participants note that triangle ACD is isosceles, with DA = DC and angles DAC = DCA.
- There is a suggestion that triangle ACM may have a 60-degree angle, but this is presented as a guess.
- Participants discuss the concept of congruence in triangles, specifically triangles ABC and MBC, and how this affects the angles in triangle ACD.
- It is proposed that the angle at C is divided into two equal angles, leading to the conclusion that angle DAC and angle DCA are both 30 degrees.
- One participant suggests a method to construct point D by copying the angle DCA at angle BAC and drawing a line through point A.
- Another participant raises a concern about copying angles with a straight edge and compass, suggesting alternative methods such as dividing line segments and using trigonometry to find lengths BD and BE.
- There is a proposal to construct a line parallel to CA through point D to find the location of point E, ensuring that ACDE forms a trapezium.
Areas of Agreement / Disagreement
Participants express various viewpoints regarding the construction methods and properties of the triangles involved. There is no clear consensus on the best approach to construct points D and E or on the angle measures, indicating that multiple competing views remain.
Contextual Notes
Some assumptions about the properties of triangles and the methods of construction are not fully resolved, particularly regarding the use of trigonometry and the limitations of the tools specified (straight edge and compass).