- #1
caffeinemachine
Gold Member
MHB
- 816
- 15
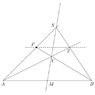
Let points $A$ and $B$ be given on the plane. The mid point of $A$ and $B$, call it $M$, is also given. Mark an arbitrary point $P$ on the plane. Using unmarked straight edge only, construct the line passing through $P$ and parallel to $AB$.