Constructibility of a Perfect Venn Diagram

[CarsonAdams]

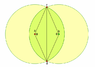
Is it possible using only a straight edge and a compass to construct a Venn Diagram or a pair of overlapping circles in which the area of the lune of each circle is equal to the other and to the area of the overlapping region?

(I've worked out most of the mathematics from calculating the area of the sector (cad) and subtracting the area of the triangle (cad) to achieve the segment of the circle created by the chord (cd) which accounts for half the total overlap. Then to achieve a useful equation, I calculated that, obviously, the area of the circle divided in half must equal twice the area of the single segment created by the chord.)

After simplifying, it would seem that to construct the required angle θ the equation
θ-sin(θ)=π/2
would have to be solved (in radians), which would seem to denote that it is not a constructible angle.

But questions of constructibility usually require someone much more clever than I, so am I missing a simplifying way to achieve this? and is it fair to say that the only way to solve the above equation is through the use of numerical methods?

*if it would be useful to review the full calculation, I can post that as well- it's just a bit tedious

 

[Simon Bridge]

To construct the diagram so all three areas are equal - you need to construct a base-line, then bisect it - the circles, of equal fixed radius (1 unit), are to intersect on that line so their centers are on the base-line. So the problem is to relate the location of the centers of the circles to the areas.

The area of the intersection region is twice the area of the circular segment cut off by the bisecting line.
Using the diagram in wikipedia: the distance from the bisector to each center is $d$.

... I don't know if this can be constructed... but it would amount to how finely you could divide lengths up.