From polar coordinates to heliocentric ecliptic coordinates

[Shukie]

So I've calculated the polar coordinates of a planet, with the sun at the origin and the x-axis being the striped line going from the sun towards point P.

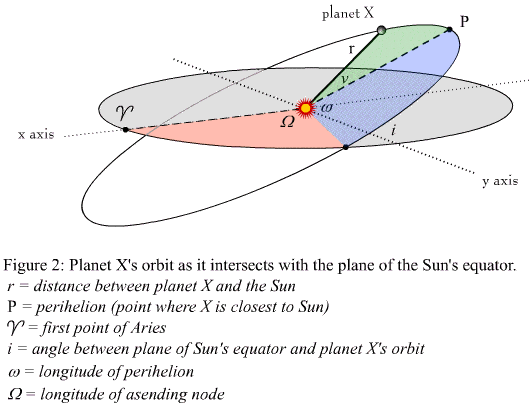
Now I have to convert these polar coordinates to heliocentric ecliptic coordinates. To do this, I have to convert to cartesian coordinates first and then rotate the plane of reference so that the x-axis will point towards $$\Upsilon$$. This is the answer:

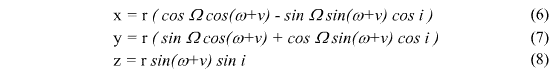
Converting to cartesian coordinates is easy, but then I'm lost. Could anyone tell me how exactly I go from $$x = r \cdot \cos{v}$$ to $$(6)$$?

 

[kuruman]

It is easier to see what's going on if you first look at the situation when the inclination $i$ is zero and then rotate the plane of the orbit away from the ecliptic. This is shown in the figure below. We have auxiliary axes $p$ from the sun to the perihelion and $q$ perpendicular to $p$. The heliocentric axes are $x$ and $y$.

We write unit vector relations
$$\begin{align} & \mathbf{\hat q}=\cos\Omega~\mathbf{\hat x}+\sin\Omega~\mathbf{\hat y}\\ & \mathbf{\hat p}=-\sin\Omega~\mathbf{\hat x}+\cos\Omega~\mathbf{\hat y}\end{align}$$The position of the planet is $$\begin{align} \mathbf{r}=r\cos(\omega+v)~\mathbf{\hat q}+r\sin(\omega+v)~\mathbf{\hat p}.\end{align}$$We now consider how these vectors change when the plane of the planet's orbit is rotated away from the ecliptic about the $q$-axis to inclination angle $i$. Only unit vecor $\mathbf{p}$ will change form. It will be off the plane of the ecliptic. Noting that its projection on the ecliptic is along its old direction. We have$$\begin{align}\mathbf{\hat p'}=\cos i (-\sin\Omega~\mathbf{\hat x}+\cos\Omega~\mathbf{\hat y})+\sin i~\mathbf{\hat z}.\end{align}$$We obtain the position of the planet in heliocentric coordinates in the inclined plane using equation (3) in which $\mathbf{\hat p}$ is replaced with $\mathbf{\hat p'}$ from equation (4) and $\mathbf{\hat q}$ from equation (1). We get $$ \mathbf{r}=r\cos(\omega+v)~( \cos\Omega~\mathbf{\hat x}+\sin\Omega~\mathbf{\hat y} )+r\sin(\omega+v)~cos i [(-\sin\Omega~\mathbf{\hat x}+\cos\Omega~\mathbf{\hat y})+\sin i~\mathbf{\hat z}]$$Separation of the cartesian components provides the desired relations.