Avocado
- 6
- 0
I calculated FS Model using Mathcad and I got that this part
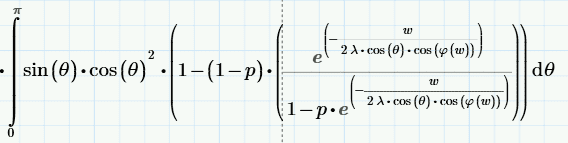
increases with decreasing width $\w$.
This make the resistivity increases with decreasing width $\w$.
This contradict the result of this model.
Has anyone ever come across with this before?
the original paper: https://journals.aps.org/prb/abstract/10.1103/PhysRevB.61.14215
complete equation:
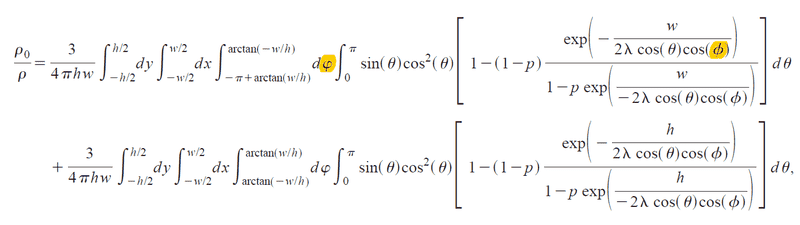
increases with decreasing width $\w$.
This make the resistivity increases with decreasing width $\w$.
This contradict the result of this model.
Has anyone ever come across with this before?
the original paper: https://journals.aps.org/prb/abstract/10.1103/PhysRevB.61.14215
complete equation:
