RemotePhysics
Gold Member
- 22
- 3
- Homework Statement
- A car is turning a banked corner, which is inclined at theta degrees (see diagram). For this particular case friction, F is not negligible and the car is going sufficiantly quickly that the friction is contributing to the centripital force.
a) Copy the diagram, draw and name the forces acting on the car
b) On a new diagram, divide the forces into their horizontal and vertical components
c) Hence show that mg+Fsin(theta)=Rcos(theta)
d) Show that (mv^2)/r=Fcos(theta)+Rsin(theta)
e) Refering to the equations, explain what happens if:
i) the corner is not banked. (i.e the road is flat)
ii) friction is negligible
f) Show that if friction is very small, the max velocity that the car can travel for a turn banked at
30 degrees, with a radius of 40 meters is approximately 15m/s
g) The actual max velocity for the turn could be around double that if the friction is included.
Under which circumstances could we consider the friction negligible.
- Relevant Equations
- Centripital force = mv^2/2
Friction = μR
Below is my working out. If you could have a look at my answers and see if they are correct and then advice me on how to improve my solutions for Parts I and II, and how to answer F and G with the given information. Thanks in advance!
Parts aand b are diagrams so please refer to the attached images.
Part c: They act in opposite directions on the diagram and cancel each other out. so Rcos(theta)-mg-Fsin(theta)=0. I then rearanged them to match the question.
Part d: Again the same reasoning as for part c, just different equations
Part e: Here is where I am getting slightly stuck?
Part I: Equations would be incorrect as forces would already be horizontal and vertical. As there is no angle there would be no need for sin(theta) and cos(theta)
Part II: mg=Rcos(theta) instead of mg+Fsin(theta)=Rcos(theta).
Fc-Fcos(theta)-Rsin(theta) would be invalid without friction as Fc>Rsin(theta).
Part f: Don't know which equation to use. I tried to rearrange (mv^2)/r=μRcos(theta)+Rsin(theta) for v but there is no mention of the mass of the car so I am unable to calculate the reaction force R or m. Also what consitutes as small level of friction? 0.1μ or 0.01μ?
Part g: Friction would be negligable if either the car was traveling very slowly and centripetal force was very small.
New member so please go easy on me if i have broken any rules :)
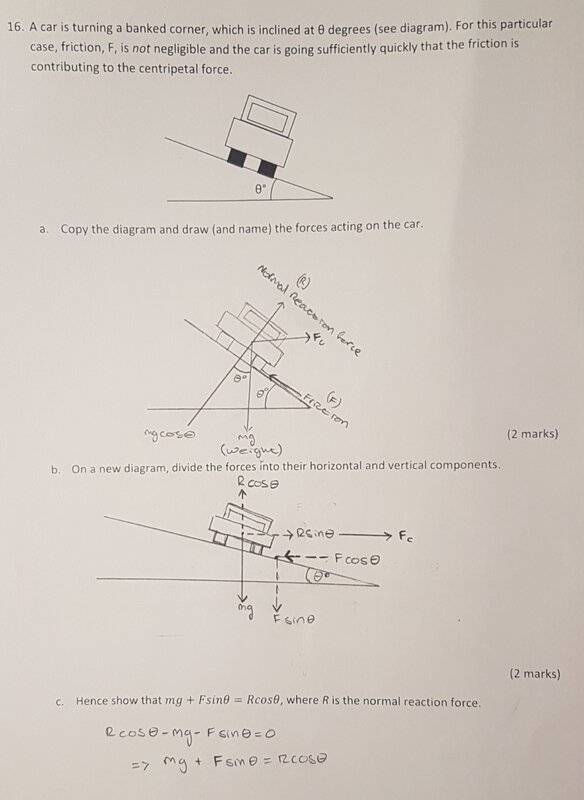


Parts aand b are diagrams so please refer to the attached images.
Part c: They act in opposite directions on the diagram and cancel each other out. so Rcos(theta)-mg-Fsin(theta)=0. I then rearanged them to match the question.
Part d: Again the same reasoning as for part c, just different equations
Part e: Here is where I am getting slightly stuck?
Part I: Equations would be incorrect as forces would already be horizontal and vertical. As there is no angle there would be no need for sin(theta) and cos(theta)
Part II: mg=Rcos(theta) instead of mg+Fsin(theta)=Rcos(theta).
Fc-Fcos(theta)-Rsin(theta) would be invalid without friction as Fc>Rsin(theta).
Part f: Don't know which equation to use. I tried to rearrange (mv^2)/r=μRcos(theta)+Rsin(theta) for v but there is no mention of the mass of the car so I am unable to calculate the reaction force R or m. Also what consitutes as small level of friction? 0.1μ or 0.01μ?
Part g: Friction would be negligable if either the car was traveling very slowly and centripetal force was very small.
New member so please go easy on me if i have broken any rules :)
Last edited by a moderator: