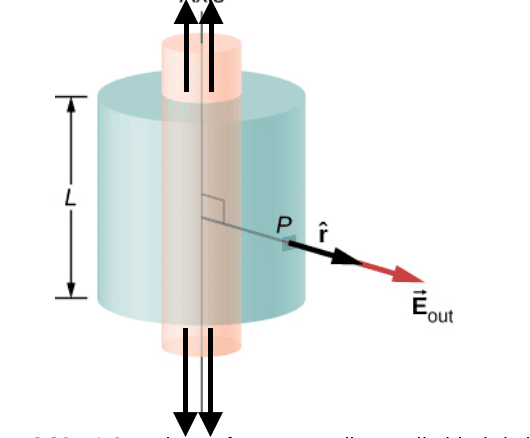
The discussion centers on the application of Gauss's Law to a finite cylindrical shell with a uniform surface charge density, denoted as ##\sigma##. Participants debate whether the lids of the Gaussian cylinder should be considered in calculating the electric field outside the shell. The consensus is that the electric field is radial and does not depend on the height of the cylinder, thus the contribution from the lids is negligible. The relevant equations include ##\lambda_{enc} = 2\pi R\sigma_0## and ##E = \frac{2\pi R\sigma_0L}{2\pi r^2 + 2\pi r L}##.
PREREQUISITESStudents of physics, particularly those studying electromagnetism, educators teaching electrostatics, and anyone seeking to deepen their understanding of Gauss's Law and its applications in real-world scenarios.
Of course we take into account the lids. What is the electric flux through each lid?annamal said:
The actual solution did not take into account the lids.kuruman said:
It is alternatively here: https://opentextbc.ca/universityphysicsv2openstax/chapter/applying-gausss-law/kuruman said:
Are you saying the problem is wrong not calculating the electric field at the lids?kuruman said:
Apart from what has already been said, it is easy to conclude that what you have done here is wrong as your result makes the field dependent on what L you pick. The actual field cannot depend on how you choose to draw your Gaussian surface.annamal said:
I wanted to give this textbook the benefit of the doubt. The solution under "Strategy" mentions "apply the Gauss's law strategy given earlier". The contribution from lids may have been discussed there and that is why I directed OP to (re)read that part. Understanding why the lids are ignored is important in understanding Gauss's law and is better achieved by discovery on one's own rather than being told.Orodruin said:
I typically doubt this since it is kind of the simplest non-spherical geometry. I agree that things are better if students can figure things out for themselves but the prevalance of students misinterpreting Gauss law as EA = Q_enc/epsilon without further qualification is way too high for me to be convenient with not giving students an example where the flux through some side is not EA. Sure, something like a pillbox around a surface charge may have been covered earlier in this particular book, but I find that it is often not the case and students are left lost and confused.kuruman said:
Gauss's law says ##q_{enc}/\epsilon_0 = EA##kuruman said:
The contribution of the lids are none if the length of the cylindrical charge is infinite. Here we have a finite lengthed Gaussian surface so there should be contribution from the lids.kuruman said:
How can the electric field just be radial when the Gaussian cylinder is of finite length L. Because the Gaussian surface has finite length, there should be electric field from the lids.Orodruin said:
No. This is not what Gauss’ law says. Gauss’ law states that the flux of the electric field through a closed surface is equal to the enclosed charge divided by epsilon_0. This is equal to EA only of the electric field is perpendicular to the surface and has the same magnitude on the entire surface.annamal said:
The field’s value does not depend on whatever Gaussian surface you choose to draw. In the case of the infinite line charge, the reflection symmetry around any plane perpendicular to the line means the field can have no component in the direction of the line. The reflection symmetry through a plane containing the line and the point where you want to know the field implies there can be no tangential component of the field.annamal said:
Please reread my post. By the symmetries of the line charge, the electric field can have no component in any direction other than the radial direction. This means that the field is parallel to the lid, which is why it is a problem that you are not saying that it is.annamal said:
Rereading this thread you seem to be under a very serious and fatal misconception that the Gaussian surface you draw somehow affects the field. It does not. The field is generated by the infinitely long line charge and the Gaussian surface has nothing to do with it. The Gaussian surface is a tool to use to help you figure out what the field generated by the line charge is by cleverly selecting what surface to use, but it carries no charge in itself and does not carry any charge. It encloses part of the charge that is carried by the line, but that is a different issue and just relates to the flux of the field out of the surface.annamal said:
I’d say it surprised me, but that would be a lie … ;)SammyS said:
