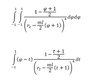Gaussian Quadrature on a Repeated Integral

[olukelliot]

Hi there,
I am having some difficulty evaluating a repeated integral, which is the first of two shown in the image.
I had hoped to be able to use Gaussian Quadrature to provide a numerical result, however am unsure on if this is possible for a repeated integral?

I have attempted to use Cauchy' formula on repeated integrals to obtain a single integral, which is shown on the bottom in the image. However I am once again unsure on performing this due to the presence of φ.

Any ideas on what I'm doing wrong/ missing?
Thanks

 

[mathman]

Your first integral is too ambiguous. You use φ for both integrations as well as as a variable in the integrand. You need to use two different symbols for the differential variables, so there would be no ambiguity for the variable in the integrand.

 

[eys_physics]

Additionally, it seems like the integral could be singular, depending on the values of $r_1$, $m$ and $l$. It is not clear from your thread what the values of these quantities are.

 

[nathal]

You have to split the repeated integral into min. two simple integrals (with different borders) and each of them could be numerical integrated by Gauss.
See:
COMPUTATION OF DEFINITE INTEGRAL OVER REPEATED INTEGRAL Katar´ina Tvrda´, Maria Minarova´
Tatra mountains matematical publications