Why Can't I Use My Indicated Vector ds on a Gaussian Surface?
- Thread starter logearav
- Start date
Click For Summary
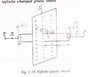
The discussion clarifies the proper orientation of the vector dS in relation to a Gaussian surface, emphasizing that dS must be perpendicular to the surface and directed outward. It highlights that the vector dS for the end caps should be drawn perpendicular to those surfaces, while the vector for the cylindrical surface is radial and also perpendicular. The electric field lines are noted to be horizontal and parallel to the curved surface of the cylinder, resulting in no flux through that part. The importance of calculating the flux through all sides of the Gaussian surface is underscored, as it often gets overlooked. The conversation concludes with appreciation for the insights provided.
Similar threads
- · Replies 9 ·
- · Replies 2 ·
- · Replies 2 ·
- · Replies 22 ·
- · Replies 2 ·
Undergrad
Pushing a rod in a magnetic field
- · Replies 15 ·
- · Replies 5 ·
- · Replies 1 ·
Undergrad
When is a water surface not dispersive?
- · Replies 1 ·