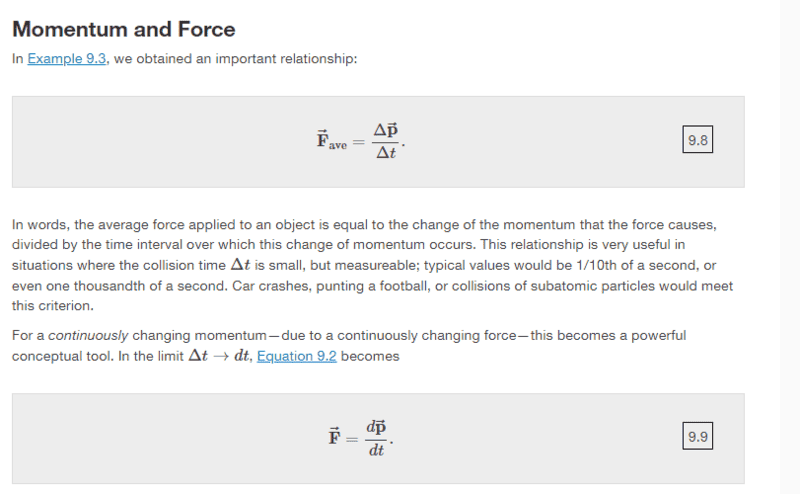
SUMMARY
The discussion focuses on deriving equation 9.9 from equation 9.8 in the context of differential calculus. Participants clarify that the limit should be taken as Δx approaches zero, rather than Δy, because the relationship between the two variables does not guarantee that Δy approaching zero implies Δx does as well. The conversation emphasizes the importance of understanding the conditions under which derivatives exist and the necessity of two-sided limits for their definition.
PREREQUISITES
- Understanding of differential calculus concepts
- Familiarity with limits and their properties
- Knowledge of derivatives and their definitions
- Basic grasp of functions and their inverses
NEXT STEPS
- Study the definition of derivatives in calculus textbooks
- Learn about the properties of limits in calculus
- Explore the concept of differentiability and its implications
- Investigate the relationship between functions and their inverses
USEFUL FOR
Students studying calculus, educators teaching differential calculus, and anyone interested in the foundational concepts of limits and derivatives.