- #1
ChiralSuperfields
- 1,206
- 132
- Homework Statement
- Please see below
- Relevant Equations
- Please see below
For this,
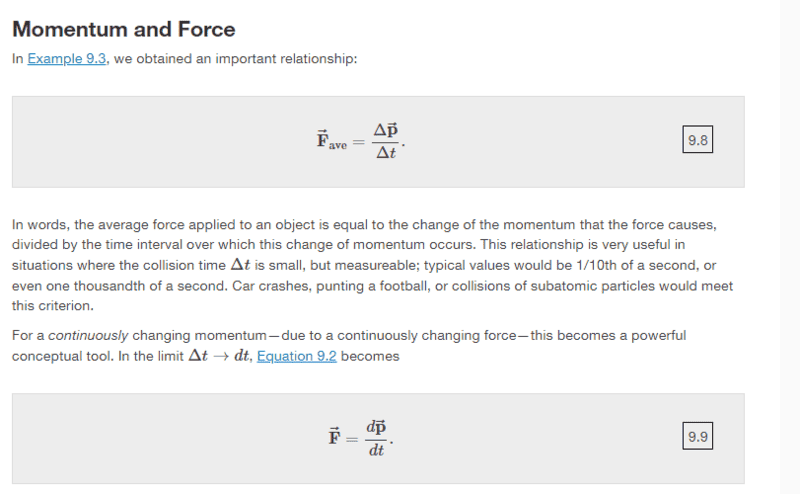
Does someone please know how do we derive equation 9.9 from 9.8? Do we take the limits as t approach's zero for both sides? Why not take limit as momentum goes to zero?
Many thanks!
Does someone please know how do we derive equation 9.9 from 9.8? Do we take the limits as t approach's zero for both sides? Why not take limit as momentum goes to zero?
Many thanks!