SUMMARY
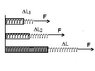
The effective force constant for two springs connected in series is calculated using the formula Keff = k1k2 / (k1 + k2). This relationship indicates that the effective spring constant is not simply the sum of the individual spring constants but rather a function of their product divided by their sum. The discussion emphasizes that while the same force acts on both springs, their extensions differ, leading to the derivation of the effective constant. Understanding this relationship is crucial for accurately modeling systems involving multiple springs in series.
PREREQUISITES
- Understanding of Hooke's Law and spring constants
- Familiarity with basic mechanics concepts
- Knowledge of algebraic manipulation for deriving equations
- Concept of effective resistance in electrical circuits for analogy
NEXT STEPS
- Study the derivation of the effective spring constant for multiple springs in series
- Explore the concept of springs in parallel and their effective constants
- Learn about the applications of spring constants in mechanical systems
- Investigate the relationship between force, extension, and energy stored in springs
USEFUL FOR
Students studying physics, mechanical engineers, and anyone involved in designing systems with spring mechanisms will benefit from this discussion.