General Solution of a Poisson Equation (maybe difficult)

[tim9000]

Hi,
This is overwhelmingly more of a maths problem than a physics problem, because it's all theoretical. I'll give some background to modle it incase the math's isn't enough.
Say you've got a planar structure of thickness 'd', lying on the z plane. Also say the upper and lower surfaces are y = 0 and y = -d, respectively.
The structure has scalar potentials inside it as so:

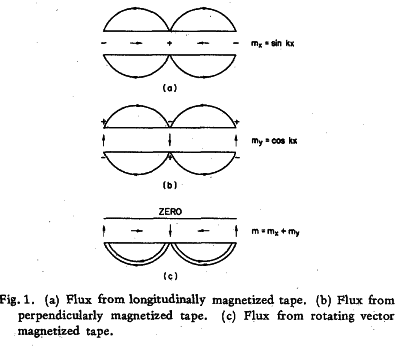
As you can see the vector fields cancel out on one side, As it says below, there is a Poisson equation of:

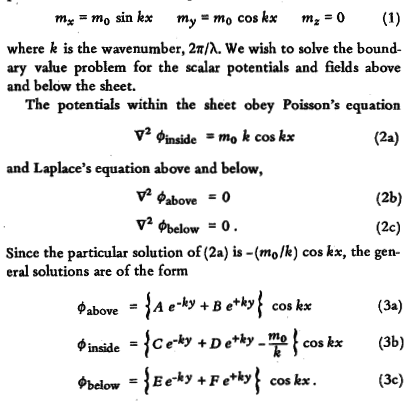
BUT I HAVE NO IDEA WHY that is the poission equation, I get that Fi_inside is a scalar potential, but why is m_ok.cos(kx) the vector field?, not like m_x+m_y or something instead? It looks like they've just differentiated m_x and that's the vector function, maybe just a coincidence?
I also have no idea how that is the general solution? Specifically the homogenious part.
I get that for the part of the particular you can solve the Poisson equation of using method of undetermined coefficients with a guess of (Asin(kx) + Bcos(kx)) and just differentiate that twice for del²:
(Asin(kx) + Bcos(kx))'' = m_ok.Cos(kx)
therefore: -A.k²sin(kx)-Bk²cos(kx) = m_ok.Cos(kx)
therefore: -A.ksin(kx)-Bkcos(kx) = m_o.Cos(kx) and equating coefficients yields:
B = - m_o/k
A = 0
so Yp = - m_o/k * Cos(kx)

But why does the homogenous part have exponentials and y in them? I thought they'd just be zero.
If someone could explain that or even just why the Poisson equation is what they say I'd be greatful.
THANKS!

P.S I also wonder, which point is chosen as x = 0 on the diagram...?

 

[SteamKing]

A Laplace equation has the form:

∇² φ = 0, where φ = f(x,y), which are also called harmonic functions.

A Poisson equation is just the non-homogeneous form of a Laplace equation, for example:

∇² φ = g (x,y) + K, where g (x,y) is a function of x and y, and K is just a constant.

These two partial differential equations see wide use in physics, particularly mechanics, hydromechanics, electrostatics, etc.

The solution to the Laplace equation φ = 0 is a trivial one and is not particularly useful.

You could also solve many ordinary differential equations using y = 0, but there could be other, non-zero solutions.

 

[tim9000]

A Laplace equation has the form:

∇² φ = 0, where φ = f(x,y), which are also called harmonic functions.

A Poisson equation is just the non-homogeneous form of a Laplace equation, for example:

∇² φ = g (x,y) + K, where g (x,y) is a function of x and y, and K is just a constant.

These two partial differential equations see wide use in physics, particularly mechanics, hydromechanics, electrostatics, etc.

The solution to the Laplace equation φ = 0 is a trivial one and is not particularly useful.

You could also solve many ordinary differential equations using y = 0, but there could be other, non-zero solutions.

Oook, I get that, but the General solution = homogenious + particular, solutions. As you can see in (3b) the particular solution I worked out is in there, but so is the 'homogenous' aspect which I can't figure out. As you can see in (2a) the Poisson is non-homogenous (not laplace) but it must use a homogenous part in the method of undetermined coefficients, I expect, to find (3a) and (3c) as well as the afformentioned aspect of (3b).

 

[SteamKing]

Oook, I get that, but the General solution = homogenious + particular, solutions. As you can see in (3b) the particular solution I worked out is in there, but so is the 'homogenous' aspect which I can't figure out. As you can see in (2a) the Poisson is non-homogenous (not laplace) but it must use a homogenous part in the method of undetermined coefficients, I expect, to find (3a) and (3c) as well as the afformentioned aspect of (3b).

There are whole classes of fundamental solutions to the Laplace equation. Selecting which fundamental solution depends on the boundary conditions of the problem under consideration. All of this is covered in the study of potential theory:

http://en.wikipedia.org/wiki/Laplace's_equation

These fundamental solutions include complex analytic functions and combinations of trig and exponential functions, as seen in the OP.

Without studying the rest of your text, I think you are expected to take it on faith that the equations describing this particular problem have the solutions shown. If you should later study potential theory, then that course will go into more detail about the fundamental solutions to the Laplace equation and how they are derived.

 

[tim9000]

There are whole classes of fundamental solutions to the Laplace equation. Selecting which fundamental solution depends on the boundary conditions of the problem under consideration. All of this is covered in the study of potential theory:

http://en.wikipedia.org/wiki/Laplace's_equation

These fundamental solutions include complex analytic functions and combinations of trig and exponential functions, as seen in the OP.

Without studying the rest of your text, I think you are expected to take it on faith that the equations describing this particular problem have the solutions shown. If you should later study potential theory, then that course will go into more detail about the fundamental solutions to the Laplace equation and how they are derived.

The boundary conditions are given later so I didn't think they were used to find the general solution. It would seem weird that I can find half of the solution and not the rest. And that doesn't explain how they came to that value of the Poisson equation.