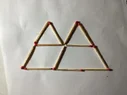bob012345
Gold Member
- 2,336
- 1,062
TL;DR: A little geometric puzzle with matches.
This puzzle is adapted from 100 Geometric Games by Pierre Berloquin. Twelve matches are arranged as in the image. Can you change the position of four matches to exactly form three equilateral triangles? Do not remove any of the matches.

This puzzle is adapted from 100 Geometric Games by Pierre Berloquin. Twelve matches are arranged as in the image. Can you change the position of four matches to exactly form three equilateral triangles? Do not remove any of the matches.