Geometrical optics: using Snell's law, find the depth of the pool

In summary, we learned that α=30°, l=0.5 m, n1=1, and n2=1.33. Using Snell's law and the given values, we found that β=60°, γ≈41°, and θ≈19°. However, the equation tan(θ+γ)=l/h is not correct. The correct expression is tan(θ+γ)= (l+x)/h, where x is the distance from the coin to the vertical line.
  • #1
tomceka
5
0
Homework Statement
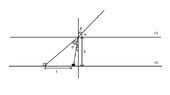
A person looks at the surface of water with an angle of 30 degrees and sees a coin 0.5 m further than it really is. What is the depth (h) of the pool.
The answer I should get is around 16 cm, but I get 0.289 m. What is wrong with my solution?
Relevant Equations
Snell's law; basic trigonometry
α=30°; l=0.5 m; n1=1; n2=1.33

α+β=90°, so β=90°-30°=60°.
Using Snell's law:
sinβ/sinγ = n2/n1
sinγ≈0.651
γ≈41°.

β=γ+θ (vertical angles)
θ=60°-41°=19°

tan(θ+β)=l/h
h=l/tan(θ+γ)
h=0.5/(tan(19+41))≈0.289 m
 

Attachments

  • photos.png
    photos.png
    2.6 KB · Views: 99
Last edited:
Physics news on Phys.org
  • #2
Welcome!
Why θ+β?
 
  • #3
Lnewqban said:
Welcome!
Why θ+β?
My bad, it should be θ+γ. Although the answer is still wrong. Is there something I missed?
 
Last edited:
  • #4
The equation tan(θ+γ)=l/h is not correct.
The coin is resting at a point far from the vertical line.
 
  • #5
Do you mind explaining what do you mean by that? Is there something wrong with my diagram?
 
  • #6
tomceka said:
Do you mind explaining what do you mean by that? Is there something wrong with my diagram?
The diagram is fine. It's your trig based on it that is not. Let x = distance from the coin to the vertical line. There is a right triangle that has angle γ and ##x## is opposite to it. Then the correct expression is, ##\tan(\theta+\gamma)=\dfrac{l+x}{h}##.
 
  • Like
Likes Lnewqban
  • #7
kuruman said:
The diagram is fine. It's your trig based on it that is not. Let x = distance from the coin to the vertical line. There is a right triangle that has angle γ and ##x## is opposite to it. Then the correct expression is, ##\tan(\theta+\gamma)=\dfrac{l+x}{h}##.
Thank you.
 

FAQ: Geometrical optics: using Snell's law, find the depth of the pool

What is Snell's law and how is it used in geometrical optics?

Snell's law is a fundamental principle in geometrical optics that describes how light rays behave when they pass through different mediums. It states that the ratio of the sine of the angle of incidence to the sine of the angle of refraction is equal to the ratio of the refractive indices of the two mediums. This law is used to calculate the direction and intensity of light rays as they pass through different materials, such as air, water, or glass.

How is Snell's law applied to finding the depth of a pool?

To find the depth of a pool using Snell's law, we first need to measure the angle of incidence of a light ray as it enters the water from above the pool's surface. We also need to know the refractive index of the water, which is approximately 1.33. Then, using Snell's law, we can calculate the angle of refraction and use simple trigonometry to find the depth of the pool. This method assumes that the pool has a flat bottom and that the light ray travels in a straight line.

How accurate is the depth measurement using Snell's law?

The accuracy of the depth measurement using Snell's law depends on the accuracy of the measurements of the angle of incidence and the refractive index of the water. If these values are measured precisely, the depth calculation can be accurate. However, this method may not be suitable for pools with uneven bottoms or if the light ray is not traveling in a straight line.

Can Snell's law be used to find the depth of any body of water?

Snell's law can be used to find the depth of any body of water, as long as the medium through which the light ray passes has a known refractive index. However, this method may not be suitable for bodies of water with varying densities or if the light ray does not travel in a straight line.

Are there any other methods for finding the depth of a pool?

Yes, there are other methods for finding the depth of a pool, such as using sonar or depth sensors. These methods may be more accurate and reliable than using Snell's law, especially for pools with irregular shapes or if the water is not clear. However, Snell's law can still be a useful tool for estimating the depth of a pool in certain situations.

Similar threads

Solve Depth of Pool w/ Snell's Law
Replies
7
Views
2K
Snell's law question with a twist....
Replies
2
Views
2K
Red and Violet Light through a Prism (Snell's Law)
Replies
6
Views
9K
Calculating Water Depth Using Snell's Law and Trigonometry
Replies
4
Views
2K
The smallest angle flashlight beam can make with horizontal
Replies
5
Views
4K
Using Snell's law to find the entering/exiting rays' angles
Replies
6
Views
9K
Calculating Apparent Depth Using Snell's Law
Replies
5
Views
14K
Optics question - Don't know if anyone can help
Replies
2
Views
1K
Finding the Velocity of Light through an Unknown substance
Replies
2
Views
8K
Solve Snell's Law Problem: 2.1m Deep Pool
Replies
2
Views
8K

Hot Threads

Recent Insights

Back
Top