Discussion Overview
The discussion revolves around the geometric and algebraic proof of the claim that if a square fits exactly within a triangle, at least two sides of that triangle must be of equal length. The scope includes geometric reasoning and algebraic justification, with participants exploring various configurations and assumptions related to the problem.
Discussion Character
- Exploratory
- Debate/contested
- Conceptual clarification
Main Points Raised
- One participant asserts that if a square fits within a triangle, at least two sides of the triangle must be equal, seeking geometric and algebraic explanations.
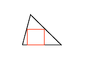
- Another participant questions the validity of the claim by presenting a counterexample, suggesting that the assertion may not hold in all cases.
- Some participants propose that the conditions of the problem may specify that the square aligns with the midpoint of one of the triangle's sides, which could support the claim.
- A clarification is made that only one side of the square should touch a side of the triangle, while the other two sides touch one of the square's corners, which raises further questions about the configuration.
- There is uncertainty about the implications of different configurations and whether they lead to two sides of the triangle being equal.
Areas of Agreement / Disagreement
Participants express differing views on the validity of the original claim, with some supporting it under specific conditions while others present counterexamples that challenge its universality. The discussion remains unresolved, with no consensus reached.
Contextual Notes
Participants note that the problem's conditions are not fully defined, leading to ambiguity in interpretations of how the square fits within the triangle. There are also unresolved questions about the geometric configurations that could affect the validity of the claim.