adjacent
Gold Member
- 1,552
- 62
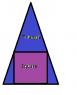
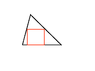
As you see in the attachment if a square exactly fits in a triangle of any shape,Then atleast Two sides of that triangle would be of equal length(Upper two sides as in attachment)
Explain this Geometrically and algebraically
I tried it but in vain(Im a 9th grader)
Explain this Geometrically and algebraically
I tried it but in vain(Im a 9th grader)
Attachments
Last edited: