Geometry problem. Circle and parallel lines to a circle.

[naggy]

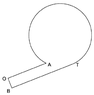
A circle with diameter 90 is located at (70,100). A given point O is at (0,0). There is a line from O to the circle at point A, line OA. Line BT is parallel to OA at a distance 50 from OA and is a tangent to the circle.

How do I find the coordinates A and B?
I'm having problems drawing this so I can find A and B. Is there a way to do it?

 

[HallsofIvy]

Let (a, b) be the coordinates of point B. Any line through (a, b) is of the form y= m(x- a)+ b for some slope m. A circle with radius 90, with center at (70, 100) (I assume that is what you mean by saying the circle is "located at (70, 100)") has equation
[tex](x- 70)^2+ (y- 100)^2= 90^2[/itex].
Putting y= m(x- a)+ b into that gives
[tex](x- 70)^2+(m(x-a)- 70+b)^2= 90[/itex]
a quadratic equation for x where the line intersects the circle. A quadratic equaton can have: no real solutions (if the line does NOT intersect the circle), one solution (if the line is tangent to the circle), two solutions (if the line crosses through the circle). Here we want the line tangent to the circle which means there must be one solution and so the "discriminant" must be 0. That gives a condition relating a, b, and m. We can also find (x, y) at the intersection in terms of a, b, and m and find the equation of the line from the center of the circle, (70, 100) to (x,y). Of course, that line is perpendicular to the tangent line and so its slope must be -1/m. That gives another equation relating a, b, and m. Finally, the line from O to B is parallel to the radius and so also slope -1/m. That gives a third equation for a, b, and m. You should be able to solve those three equations for a, b, and m. (a, b) is, of course, B. The line OA will be y= mx with the same m you have just found. Solve the equations y= mx and $(x- 70)^2+ (y- 100)^2= 90^2$ for the x and y of point A.